
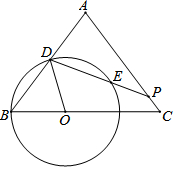
 如图,已知△ABC中,AB=AC=5,BC=6,点O是边BC上的动点,以点O为圆心,OB为半径作圆O,交AB边于点D,过点D作∠ODP=∠B,交边AC于点P,交圆O与点E.设OB=x.
如图,已知△ABC中,AB=AC=5,BC=6,点O是边BC上的动点,以点O为圆心,OB为半径作圆O,交AB边于点D,过点D作∠ODP=∠B,交边AC于点P,交圆O与点E.设OB=x.分析 (1)如图1中,首先求出cos∠B,cos∠A,如图2中,当点P与C重合时,只要证明PA=PD即可;
(2)如图2中,作CG⊥AB于G,OH⊥BD于H.分两种情形①当$\frac{11}{6}$≤x≤$\frac{625}{234}$时,如图4中.②当$\frac{625}{234}$<x<$\frac{25}{6}$时,如图5中,作PG⊥AB于G.
(3)如图6中,连接OP.根据cos∠C=cos∠B=$\frac{PC}{OC}$=$\frac{3}{5}$,列出方程,求出两圆的半径,圆心距即可判断.
解答 解:(1)如图1中,作AH⊥BC于H,CG⊥AB于G,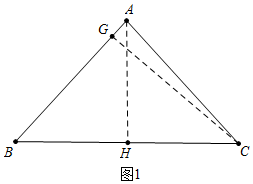
∵AB=AC=5,AH⊥BC,
∴BH=CH=3,AH=4,
∵$\frac{1}{2}$•BC•AH=$\frac{1}{2}$•AB•CG,
∴CG=$\frac{24}{5}$,AG=$\sqrt{A{C}^{2}-C{G}^{2}}$=$\frac{7}{5}$,
∴cos∠B=$\frac{3}{5}$,cos∠BAC=$\frac{7}{25}$,
如图2中,当点P与C重合时,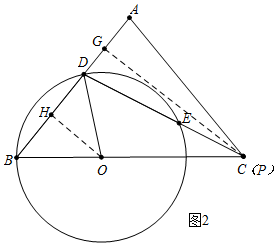
∵OB=OD,
∴∠B=∠ODB=∠ACB,
∵∠ADO=∠B+∠BOD=∠CDO+∠ADP,∠ODP=∠B,
∴∠ADP=∠BOD=∠BAC,
∴PA=PD=5;
(简单解法:易知∠A=180°-2∠B,只要证明∠ADP=180°-2∠B即可解决问题)
(2)如图2中,作CG⊥AB于G,OH⊥BD于H.
∵AD=2AG=$\frac{14}{5}$,
∵BD=2BH=2OB•cos∠B=$\frac{6}{5}$x,
∴$\frac{6}{5}$x+$\frac{14}{5}$=5,
∴x=$\frac{11}{6}$,
如图3中,当P、E重合时,作EG⊥AD于G.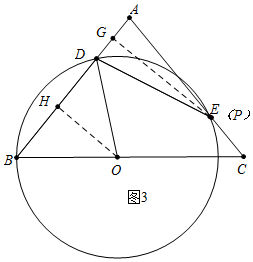
根据对称性可知,B、E关于直线OD对称,
∴DB=DE=AE=$\frac{6}{5}$x,
∵cos∠A=$\frac{7}{25}$=$\frac{AG}{AE}$,
∴$\frac{\frac{5-\frac{6}{5}x}{2}}{\frac{6}{5}x}$=$\frac{7}{25}$,
解得x=$\frac{625}{234}$,
当点D与A重合时$\frac{6}{5}$x=5,
∴x=$\frac{25}{6}$,
当$\frac{11}{6}$≤x≤$\frac{625}{234}$时,如图4中,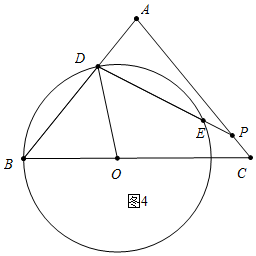
∵y=PA-PE=PD-PE=DE=BD=$\frac{6}{5}$x,
∴y=$\frac{6}{5}$x,
当$\frac{625}{234}$<x<$\frac{25}{6}$时,如图5中,作PG⊥AB于G.
∵BD=DE=$\frac{6}{5}$x,DG=AG=$\frac{1}{2}$(5-$\frac{6}{5}$x),
∴AP=AG÷cos∠A=$\frac{25}{14}$(5-$\frac{6}{5}$x),
∴y=AP-EP=$\frac{25}{14}$(5-$\frac{6}{5}$x)-[$\frac{6}{5}$x-$\frac{25}{14}$(5-$\frac{6}{5}$x)]=-$\frac{192}{35}$x+$\frac{125}{7}$,
综上所述,y=$\left\{\begin{array}{l}{\frac{6}{5}x}&{(\frac{11}{6}≤x≤\frac{625}{234})}\\{-\frac{192}{35}x+\frac{125}{7}}&{(\frac{625}{234}<x<\frac{25}{6})}\end{array}\right.$.
(3)如图6中,连接OP.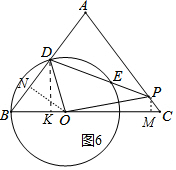
连接OP,作DK⊥OB,ON⊥BD、PM⊥BC于M,设ON=4k,则易知OB=DO=5k.BN=DN=3k,
DK=$\frac{BD•ON}{OB}$=$\frac{24}{5}$k,OP=$\frac{20}{3}$k,
由△DOK∽△OPM可得OM=$\frac{32}{5}$k,PM=$\frac{28}{15}$k,可得PC=$\frac{7}{3}$k,
∵OD+PC=5k+$\frac{7}{3}$k=$\frac{22}{3}$k>$\frac{20}{3}$k,
∴以点P为圆心,PC为半径的圆P与圆O的位置关系是相交.
点评 本题考查圆综合题、锐角三角函数、等腰三角形的判定和性质等知识,解题的关键是寻找特殊点解决问题,学会构建方程的解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC三个顶点的坐标分别为A(-1,3),B(-4,1),C(-2,1).
如图,△ABC三个顶点的坐标分别为A(-1,3),B(-4,1),C(-2,1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的①③④⑤(把你认为正确结论的序号都填上)
如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的①③④⑤(把你认为正确结论的序号都填上)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com