
如图,一个直角三角形纸片的顶点
A在∠MON的边OM上移动,移动过程中始终保持AB⊥ON于点B,AC⊥OM于点A.∠MON的角平分线OP分别交AB、AC于D、E两点.
(1)
点A在移动的过程中,线段AD和AE有怎样的数量关系,并说明理由.(2)
点A在移动的过程中,若射线ON上始终存在一点F与点A关于OP所在的直线对称,判断并说明以A、D、F、E为顶点的四边形是怎样特殊的四边形?(3)
若∠MON=45°,猜想线段AC、AD、OC之间有怎样的数量关系,并证明你的猜想.|
(1)AE=AD 2分 (2)菱形 3分 (法一):连接DF、EF ∵点 F与点A关于直线OP对称,E、D在OP上, ∴ AE=FE,AD=FD 5分由 (1)得AE=AD∴ AE=FE=AD=FD∴四边形 ADFE是菱形 7分(法二):连接AF交DE于点G,连接DF,EF.点F与点A关于直线OP对称可知:AF⊥DE,AE=FE, 3分 ∴ AG=FG,又∵ AE=AD∴ DG=EG∴四边形 ADFE是平行四边形 6分∵ AF⊥DE∴平行四边形 ADFE是菱形 7分(3)OC=AC+AD 8分 (法一):证明:连接EF ∵点 F与点A关于直线OP对称,∴ AO=OF∵ AC⊥OM,∠MON=45°∴∠ OAC=90°∴∠ ACO=∠MON=45°∴ OF=AO=AC 10分由 (2)知四边形ADFE是菱形∴ EF∥AB,AD=EF∵ AB⊥ON∴∠ ABC=90°∴∠ EFC=∠ABC=90°∵∠ ACO=45°∴∠ ACO=∠CEF∴ FC=EF=AD又∵ OC=OF+FC∴ OC=AC+AD 12分
(法2)证明:连接EF ∵ AC⊥OM,∠MON=45°∴∠ OAC=90°∴∠ ACO=∠MON=45°∴ AO=AC由 (2)知四边形ADFE是菱形∴ EF∥ABAD=EF∵ AB⊥ON∴∠ ABC=90°∴∠ EFC=∠ABC=90°∵∠ ACO=45°∴∠ FEC=∠ACO=45° 9分∴ FC=FE=AD∵∠ AOE=∠FOE∵ OE=OE,∠OAC=∠OFE=90°∵△ OAE≌△OFE 11分∴ OA=OF∴ OF=AC又∵ OF+FC=OC∴ AC+AD=OC 12分
(法3)证明:延长EA到G点,使AG=AE ∵∠ OAE=90°∴ OA⊥GE∴ OG=OE∴∠ AOG=∠EOA∵∠ AOC=45°,OP平分∠AOC∴∠ AOE=22.5°∴∠ AOG=22.5°∠G=67.5°∴∠ COG=∠G=67.5°∴ CG=OC 10分由 (1)得AD=AE∵ AD=AE=AG∴ AC+AD=OC 12分
|


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
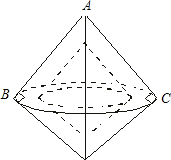 如图,一个直角三角形纸板,其两条直角边长分别为6cm和8cm,小明以纸板的斜边为旋转轴旋转这个三角形纸板形成如图所示的旋转体.请你帮小明推算出这个旋转体的全面积.(π取3.14)
如图,一个直角三角形纸板,其两条直角边长分别为6cm和8cm,小明以纸板的斜边为旋转轴旋转这个三角形纸板形成如图所示的旋转体.请你帮小明推算出这个旋转体的全面积.(π取3.14)查看答案和解析>>
科目:初中数学 来源: 题型:
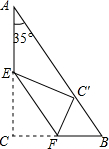 如图是一个直角三角形的纸片,将直角沿EF折叠,使C点落在AB边上,并且使∠EC′A=∠A,那么∠C′FE的度数是( )
如图是一个直角三角形的纸片,将直角沿EF折叠,使C点落在AB边上,并且使∠EC′A=∠A,那么∠C′FE的度数是( )| A、50° | B、45° | C、55° | D、70°第7题图 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com