
分析 (1)先把括号里的式子进行通分,再把除法转化成乘法,然后约分,最后把x,y的值代入计算即可;
(2)先把$\frac{1}{2}$a3b+a2b2+$\frac{1}{2}$ab3提公因式$\frac{1}{2}$ab,再运用完全平方和公式分解因式,最后整体代入求值.
解答 解:(1)$(\frac{1}{x+y}+\frac{1}{y-x})÷\frac{y^2}{{xy-{y^2}}}$=[$\frac{x-y}{(x+y)(x-y)}$-$\frac{x+y}{(x+y)(x-y)}$]×$\frac{y(x-y)}{{y}^{2}}$=$\frac{-2y}{(x+y)(x-y)}$×$\frac{y(x-y)}{{y}^{2}}$=-$\frac{2}{x+y}$,
把x=-2,y=1代入上式得:
原式=-$\frac{2}{-2+1}$=2;
(2)求$\frac{1}{2}{a^3}b+{a^2}{b^2}+\frac{1}{2}a{b^3}$=$\frac{1}{2}$ab(a2+2ab+b2)=$\frac{1}{2}$ab(a+b)2,
当a+b=2,ab=2时,
原式=$\frac{1}{2}$×2×22=4.
点评 此题考查了分式的化简求值,化简求值是课程标准中所规定的一个基本内容,它涉及对运算的理解以及运算技能的掌握两个方面,也是一个常考的题材.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
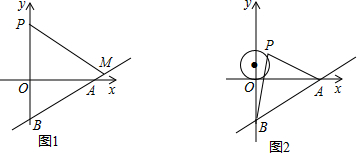
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月份 | 用电量(千瓦时) | 交电费总数(元) |
| 2 | 80 | 25 |
| 3 | 40 | 10 |
| 4 | 90 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
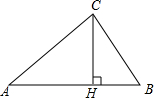 如图,学校有一块三角形草坪,数学课外小组的同学测得其三边的长分别为AB=200米,AC=160米,BC=120米.
如图,学校有一块三角形草坪,数学课外小组的同学测得其三边的长分别为AB=200米,AC=160米,BC=120米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com