
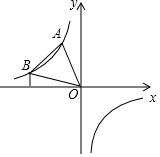
 如图,已知A,B两点都在反比例函数y=-$\frac{8}{x}$位于第二象限内的图象上,且△OAB为等边三角形,则△OAB的面积为( )
如图,已知A,B两点都在反比例函数y=-$\frac{8}{x}$位于第二象限内的图象上,且△OAB为等边三角形,则△OAB的面积为( )| A. | 4$\sqrt{3}$cm2 | B. | 6$\sqrt{3}$cm2 | C. | 8$\sqrt{3}$cm2 | D. | 12$\sqrt{3}$cm2 |
分析 设点A的坐标为(m,-$\frac{8}{m}$),点B的坐标为(n,-$\frac{8}{n}$),根据等边三角形的性质即可得出OA=OB=AB,即$\sqrt{{m}^{2}+\frac{64}{{m}^{2}}}$=$\sqrt{{n}^{2}+\frac{64}{{n}^{2}}}$=$\sqrt{(m-n)^{2}+(\frac{8}{n}-\frac{8}{m})^{2}}$,解之即可得出m2+$\frac{64}{{m}^{2}}$=32,再根据三角形的面积公式即可求出S△OAB的值,此题得解.
解答 解:设点A的坐标为(m,-$\frac{8}{m}$),点B的坐标为(n,-$\frac{8}{n}$), 则m<0,n<0.
则m<0,n<0.
∵△OAB为等边三角形,
∴OA=OB=AB,即$\sqrt{{m}^{2}+\frac{64}{{m}^{2}}}$=$\sqrt{{n}^{2}+\frac{64}{{n}^{2}}}$=$\sqrt{(m-n)^{2}+(\frac{8}{n}-\frac{8}{m})^{2}}$,
∴mn=8,m2+$\frac{64}{{m}^{2}}$=32.
∴S△OAB=$\frac{\sqrt{3}}{4}$OA2=$\frac{\sqrt{3}}{4}$(m2+$\frac{64}{{m}^{2}}$)=$\frac{\sqrt{3}}{4}$×32=8$\sqrt{3}$.
故选C.
点评 本题考查了等边三角形的性质以及反比例函数图象上点的坐标特征,根据等边三角形的性质找出m2+$\frac{64}{{m}^{2}}$=32是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
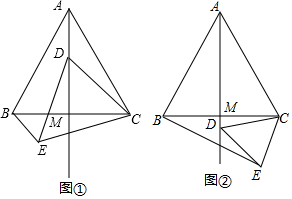
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
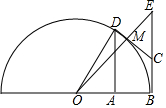 如图,在半⊙O中,∠BOD=60°,DA⊥OB,EB是切线,OE交弧BD于点M,点C在BE上,∠BOE=∠MCE=45°,连接CM.若BC=1,则AB=$\frac{1}{2}$($\sqrt{2}$+1).
如图,在半⊙O中,∠BOD=60°,DA⊥OB,EB是切线,OE交弧BD于点M,点C在BE上,∠BOE=∠MCE=45°,连接CM.若BC=1,则AB=$\frac{1}{2}$($\sqrt{2}$+1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
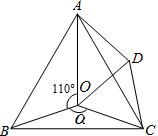 如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.
如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com