
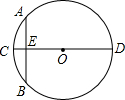
 “圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,求直径CD的长”.(1尺=10寸)则CD=26寸.
“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,求直径CD的长”.(1尺=10寸)则CD=26寸.  探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | ( 3a-b)2 | B. | (3b+a)2 | C. | (3b-a)2 | D. | ( 3a+b)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,-1) | B. | ($\frac{1}{3}$,3) | C. | (-3,-1) | D. | (-$\frac{1}{3}$,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 近似数1.8与1.80表示的意义不一样 | |
| B. | 5.0万精确到万位 | |
| C. | 0.20精确到0.01 | |
| D. | 0.345×105用科学记数法表示为3.45×104 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com