
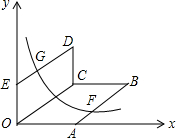
 如图,0为原点,A(4,0),E(0,3),四边形OABC,四边形OCDE都为平行四边形,OC=5,函数y=$\frac{k}{x}$(x>0)的图象经过AB的中点F和DE的中点G,则k的值为9.
如图,0为原点,A(4,0),E(0,3),四边形OABC,四边形OCDE都为平行四边形,OC=5,函数y=$\frac{k}{x}$(x>0)的图象经过AB的中点F和DE的中点G,则k的值为9. 分析 (1)根据两平行四边形对边平行且相等可知:OE=3,OA=4,并由设出C、B、D的坐标;
(2)表示出点F和G的坐标,并根据反比例函数列等式,求出a与b的关系:3a=4b,a=$\frac{4b}{3}$;
(3)由OC的长及点C的坐标列式:a2+b2=52,求出a与b的值;
(4)写出点G或点F的坐标,计算k的值.
解答 解:∵A(4,0),E(0,3),
∴OE=3,OA=4,
由?OABC和?OCDE得:OE∥DC,BC∥OA且DC=OE=3,BC=OA=4,
设C(a,b),则D(a,b+3)、B(4+a,b),
∵AB的中点F和DE的中点G,
∴G($\frac{a}{2},\frac{b+6}{2}$),F($\frac{8+a}{2},\frac{b}{2}$),
∵函数y=$\frac{k}{x}$(x>0)的图象经过点G和F,
则$\frac{a}{2}•\frac{b+6}{2}=\frac{8+a}{2}•\frac{b}{2}$,
3a=4b,a=$\frac{4b}{3}$,
∵OC=5,C(a,b),
∴a2+b2=52,
$(\frac{4b}{3})^{2}+{b}^{2}={5}^{2}$,b=±3,
∵b>0,
∴b=3,a=4,
∴F(6,$\frac{3}{2}$),
∴k=6×$\frac{3}{2}$=9;
故答案为:9.
点评 本题考查了平行四边形及反比例函数的性质,根据坐标特点及平行四边形对边平行相等的性质,利用点C的坐标表示出点B和D的坐标是本题的突破口,找出两组等量关系列方程是本题的关键;同时利用待定系数法求反比例函数的比例系数.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
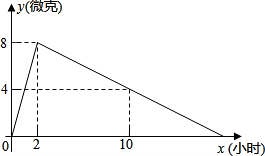 某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升8微克(1000微克=1毫克),接着逐步衰减,10小时时血液中含药量为每毫升4微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示.当成人按规定剂量服药后:
某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升8微克(1000微克=1毫克),接着逐步衰减,10小时时血液中含药量为每毫升4微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示.当成人按规定剂量服药后:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在如图所示的平面直角坐标系中,一只蚂蚁从A点出发,沿着A-B-C-D-A…循环爬行,其中A点坐标为(1,-1),B的坐标为(-1,-1),C的坐标为(-1,3),D的坐标为(1,3),当蚂蚁爬了2015个单位时,它所处位置的坐标为(1,0).
在如图所示的平面直角坐标系中,一只蚂蚁从A点出发,沿着A-B-C-D-A…循环爬行,其中A点坐标为(1,-1),B的坐标为(-1,-1),C的坐标为(-1,3),D的坐标为(1,3),当蚂蚁爬了2015个单位时,它所处位置的坐标为(1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 一户居民的年用气量 | 150 | 250 | 350 | … |
| 付款金额/元 | 375 | 625 | 900 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com