练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．阅读下面材料：
    在数学课上，老师提出如下问题：

    小芸的作法如下：

    老师说：“小芸的作法正确．”
    请回答：小芸的作图依据是到线段两个端点距离相等的点在线段的垂直平分线上，两点确定一条直线．．

    分析 通过作图得到CA=CB，DA=DB，则可根据线段垂直平分线定理的逆定理判断CD为线段AB的垂直平分线．

    解答 解：∵CA=CB，DA=DB，
    ∴CD垂直平分AB（到线段两个端点距离相等的点在线段的垂直平分线上，两点确定一条直线．）
    故答案为：到线段两个端点距离相等的点在线段的垂直平分线上，两点确定一条直线．．

    点评 本题考查了基本作图：基本作图有：作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    15．若不等式组$\left\{\begin{array}{l}{2＜x＜3}\\{x＜m}\end{array}\right.$无解，则m的取值范围是m≤2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．某工厂现有甲种原料360千克，乙种原料290千克，计划用这两种原料全部生产A、B两种产品共50件，生产A、B两种产品与所需原料情况如下表所示：
    原料
    型号    		 甲种原料（千克） 乙种原料（千克）
     A产品（每件） 9 3
     B产品（每件） 4 10
    （1）该工厂生产A、B两种产品有哪几种方案？
    （2）若生成一件A产品可获利80元，生产一件B产品可获利120元，怎样安排生产可获得最大利润？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．如图，在△ABC中，CA=CB，∠ACB=90°，以AB的中点D为圆心，作圆心角为90°的扇形DEF，点C恰在EF上，设∠BDF=α（0°＜α＜90°），当α由小到大变化时，图中阴影部分的面积（　　）
    A．由小到大B．由大到小
    C．不变D．先由小到大，后由大到小

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．一家游泳馆的游泳收费标准为30元/次，若购买会员年卡，可享受如下优惠：
    会员年卡类型办卡费用（元）每次游泳收费（元）
    A 类5025
    B 类20020
    C 类40015
    例如，购买A类会员年卡，一年内游泳20次，消费50+25×20=550元，若一年内在该游泳馆游泳的次数介于45～55次之间，则最省钱的方式为（　　）
    A．购买A类会员年卡B．购买B类会员年卡C．购买C类会员年卡D．不购买会员年卡

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．下面角的图示中，能与30°角互补的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

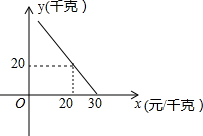    17．某超市对进货价为10元/千克的某种苹果的销售情况进行统计，发现每天销售量y（千克）与销售价x（元/千克）存在一次函数关系，如图所示．
    （1）求y关于x的函数关系式（不要求写出x的取值范围）；
    （2）应怎样确定销售价，使该品种苹果的每天销售利润最大？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．用计算器计算$\root{3}{28.36}$约为（　　）
    A．3.049B．3.050C．3.051D．3.052

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图，矩形ABCD被分成四部分，其中△ABE、△ECF、△ADF的面积分别为2、3、4，则△AEF的面积为7．

    查看答案和解析>>

    同步练习册答案