
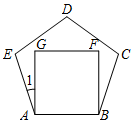
 如图放置的一个正五边形ABCDE和正方形ABFG边长相等,则∠1=18度.
如图放置的一个正五边形ABCDE和正方形ABFG边长相等,则∠1=18度. 科目:初中数学 来源: 题型:填空题
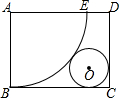 如图,将矩形纸片ABCD裁剪出扇形ABE和⊙O,其中⊙O与$\widehat{BE}$,BC,CD都相切.若扇形ABE与⊙O恰好制作成一个圆锥,已知AB=8cm,则AD的长为10.
如图,将矩形纸片ABCD裁剪出扇形ABE和⊙O,其中⊙O与$\widehat{BE}$,BC,CD都相切.若扇形ABE与⊙O恰好制作成一个圆锥,已知AB=8cm,则AD的长为10.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知直线y=-x+4与双曲线y=$\frac{k}{x}$(x>0)只有一个交点,将直线y=-x+4向上平移1个单位后与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,如图,则A点的坐标为( )
已知直线y=-x+4与双曲线y=$\frac{k}{x}$(x>0)只有一个交点,将直线y=-x+4向上平移1个单位后与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,如图,则A点的坐标为( )| A. | (1,4) | B. | (1,5) | C. | (2,3) | D. | (2,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | ±$\sqrt{2}$ | C. | 2 | D. | ±2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
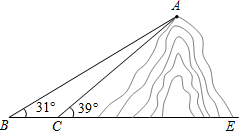 如图,小明想测山高度,他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°.求这座山的高度(小明的身高忽略不计).
如图,小明想测山高度,他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°.求这座山的高度(小明的身高忽略不计).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com