
【题目】如图,为了开发利用海洋资源,某勘测飞机预测量一岛屿两端A、B的距离,飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,求岛屿两端A、B的距离.

【答案】岛屿两端A.B的距离为(600-![]() )米.
)米.
【解析】试题分析:首先过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,易得四边形ABFE为矩形,根据矩形的性质,可得AB=EF,AE=BF.由题意可知:AE=BF=100米,CD=500米,然后分别在Rt△AEC与Rt△BFD中,利用三角函数即可求得CE与DF的长,继而求得岛屿两端A、B的距离.
试题解析:过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,

∵AB∥CD,
∴∠AEF=∠EFB=∠ABF=90°,
∴四边形ABFE为矩形.
∴AB=EF,AE=BF.
由题意可知:AE=BF=100米,CD=500米.
在Rt△AEC中,∠C=60°,AE=100米.
∴CE=![]() (米).
(米).
在Rt△BFD中,∠BDF=45°,BF=100米.
∴DF=![]() =100(米).
=100(米).
∴AB=EF=CD+DF-CE=500+100-![]() ≈600-
≈600-![]() ×1.73≈600-57.67≈542.3(米).
×1.73≈600-57.67≈542.3(米).
答:岛屿两端A、B的距离为542.3米.


科目:初中数学 来源: 题型:
【题目】课外活动时间,甲、乙、丙、丁4名同学相约进行羽毛球比赛.
(1)如果将4名同学随机分成两组进行对打,求恰好选中甲乙两人对打的概率;
(2)如果确定由丁担任裁判,用“手心、手背”的方法在另三人中竞选两人进行比赛.竞选规则是:三人同时伸出“手心”或“手背”中的一种手势,如果恰好只有两人伸出的手势相同,那么这两人上场,否则重新竞选.这三人伸出“手心”或“手背”都是随机的,求一次竞选就能确定甲、乙进行比赛的概率.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:![]() 列举出将4名同学随机分成两组进行对打所有可能的结果,找出甲乙两人对打的情况数,根据概率公式计算即可.
列举出将4名同学随机分成两组进行对打所有可能的结果,找出甲乙两人对打的情况数,根据概率公式计算即可.
![]() 画树状图写出所有的情况,根据概率的求法计算概率.
画树状图写出所有的情况,根据概率的求法计算概率.
详解:(1)甲同学能和另一个同学对打的情况有三种:
(甲、乙),(甲、丙),(甲、丁)
则恰好选中甲乙两人对打的概率为:![]()
(2)树状图如下:
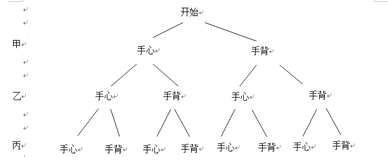
一共有8种等可能的情况,其中能确定甲乙比赛的可能为(手心、手心、手背)、(手背、手背、手心)两种情况,因此,一次竞选就能确定甲、乙进行比赛的概率为![]() .
.
点睛:考查概率的计算,明确概率的意义时解题的关键,概率等于所求情况数与总情况数的比.
【题型】解答题
【结束】
22
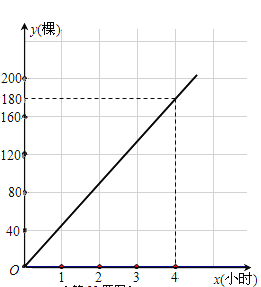
【题目】为了“绿化环境,美化家园”,3月12日(植树节)上午8点,某校901、902班同学同时参加义务植树.901班同学始终以同一速度种植树苗,种植树苗的棵数y1与种植时间x(小时)的函数图象如图所示;902班同学开始以1小时种植40棵的速度工作了1.5小时后,因需更换工具而停下休息半小时,更换工具后种植速度提高至原来的1.5倍.
(1)求902班同学上午11点时种植的树苗棵数;
(2)分别求出901班种植数量y1、902班种植数量y2与种植时间x(小时)之间的函数关系式,并在所给坐标系上画出y2关于x的函数图象;
(3)已知购买树苗不多于120棵时,每棵树苗的价格是20元;购买树苗超过120棵时,超过的部分每棵价格17元.若本次植树所购树苗的平均成本是18元,则两班同学上午几点可以共同完成本次植树任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 的位置如图所示.点A,B,C的坐标分别为
的位置如图所示.点A,B,C的坐标分别为![]() ,
,![]() ,
,![]() ,根据下面要求完成解答.
,根据下面要求完成解答.

(1)作![]() 关于点C成中心对称的
关于点C成中心对称的![]() ;
;
(2)将![]() 向右平移4个单位,作出平移后的
向右平移4个单位,作出平移后的![]() ;
;
(3)在x轴上求作一点P,使![]() 的值最小,直接写出点P的坐标.
的值最小,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年9月,小军顺利升入初中,为学习需要,准备购买若干个创意笔记本,甲、乙两家文具店都有足够数量的创意笔记本,这两家文具店创意笔记本标价都是每个8元,甲文具店的销售方案是:购买创意笔记本的数量不超过6个时,原价销售;购买创意笔记本超过6个时,从第7个开始按标价的![]() 出售;乙文具店的销售方案是:不管购买多少个创意笔记本,一律按标价的
出售;乙文具店的销售方案是:不管购买多少个创意笔记本,一律按标价的![]() 出售.
出售.
(1)若设小军要购买![]() 个创意笔记本,请用含
个创意笔记本,请用含![]() 的代数式分别表示小军到甲文具店和乙文具店购买全部创意笔记本所需的费用;
的代数式分别表示小军到甲文具店和乙文具店购买全部创意笔记本所需的费用;
(2)小军购买多少个创意笔记本时,到甲、乙两家文具店购买全部创意笔记本所需的费用相同?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 过点
过点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() 过点
过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交反比例函数图象于点
交反比例函数图象于点![]() .
.
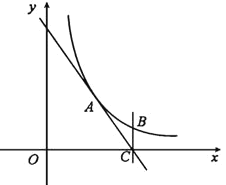
(1)求![]() 的值与
的值与![]() 点的坐标;
点的坐标;
(2)连结![]() ,求
,求![]() 的面积;
的面积;
(3)在平面内有点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() ,
,![]() 四点为顶点的四边形为平行四边形,试写出符合条件的所有
四点为顶点的四边形为平行四边形,试写出符合条件的所有![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )
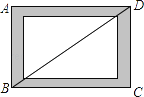
A. 四边形ABCD由矩形变为平行四边形 B. BD的长度增大
C. 四边形ABCD的面积不变 D. 四边形ABCD的周长不变
查看答案和解析>>
科目:初中数学 来源: 题型:
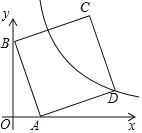
【题目】如图,在平面直角坐标系中,直线y=﹣4x+4与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,点D在双曲线y=![]() 上;将正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线在第一象限的分支上,则a的值是_____.
上;将正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线在第一象限的分支上,则a的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:某社区超市第一次用6000元购进甲、乙两种商品,其中甲商品的件数比乙商品件数的2倍少30件,甲、乙两种商品的进价和售价如表:
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原售价销售,乙商品在原售价上打折销售.第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多720元,求第二次乙种商品是按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
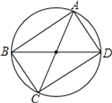
【题目】给出下面四个命题,其中真命题的个数有( )
(1)平分弦的直径垂直于这条弦,并且平分这条弦所对的弧;
(2)90°的圆周角所对的弦是直径;
(3)在同圆或等圆中,圆心角的度数是圆周角的度数的两倍;
(4)如下图,顺次连接圆的任意两条直径的端点,所得的四边形一定是矩形.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com