
【题目】如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点是法国数学家和教育家克洛尔于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=。
【答案】![]()
【解析】解 :如图,在等腰直角三角形△DEF中,∠EDF=90,DE=DF,∠1=∠2=∠3, 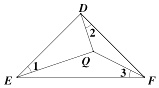
∴∠1+∠QEF=∠3+∠DFQ=45,
∴∠QEF=∠DFQ;sin45°=DF∶EF=1∶![]()
又∵∠2=∠3,
∴△DQF∽△FQE,
∴DQ∶FQ=FQ∶QE=DF∶EF=1∶![]() ,
,
∵DQ=1,
∴FQ=![]() ,EQ=2,
,EQ=2,
∴EQ+FQ=2+![]() ,
,
由等腰直角三角形的性质得出∠1+∠QEF=∠3+∠DFQ=45,进而得出∠QEF=∠DFQ;sin45°=DF∶EF=1∶![]() ,然后判断出△DQF∽△FQE,根据相似三角形对应边成比例得出DQ∶FQ=FQ∶QE=DF∶EF=1∶
,然后判断出△DQF∽△FQE,根据相似三角形对应边成比例得出DQ∶FQ=FQ∶QE=DF∶EF=1∶![]() ,进而求出FQ=
,进而求出FQ=![]() ,EQ=2,从而得出答案。
,EQ=2,从而得出答案。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1 000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟.其中正确的说法是_________________(把你认为正确说法的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,O为平面直角坐标系的原点,点的坐标分别为A(a,2)、B(a,-1),D(b,2).且a、b满足![]() .点P从A点出发,以每秒1个单位长度的速度A-B-C-D-A的线路移动,运动时间为t,当点P回到A点时运动停止
.点P从A点出发,以每秒1个单位长度的速度A-B-C-D-A的线路移动,运动时间为t,当点P回到A点时运动停止
(1)点C的坐标为_______________
(2)当点P移动在线段BC上时,求三角形ACP的面积(用含t的代数式表示)
(3)在移动过程中,当三角形ACP的面积是5时,直接写出点P移动的时间为几秒

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABD、∠ACD的角平分线交于点P,若∠A = 50°,∠D =10°,则∠P的度数为( )
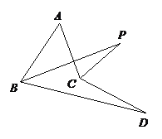
A.15°B.20°C.25°D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,C、E是⊙O上的点, CD⊥AB,EF⊥AB,垂足分别为D、F,过点E作 EG⊥0C,垂足为G,延长EG交OA于H。
求证:
(1)HO·HF=HG·HE;
(2)FG=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD、MN相交与点O,FO⊥BO,OM平分∠DOF
(1)请直接写出图中所有与∠AON互余的角: .
(2)若∠AOC=![]() ∠FOM,求∠MOD与∠AON的度数.
∠FOM,求∠MOD与∠AON的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com