
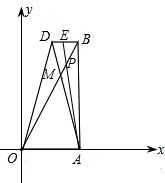
 对角线OB,AD相交于点M.OA=2,AB=2
对角线OB,AD相交于点M.OA=2,AB=2| 3 |
| 3 |
| BM |
| OM |
| 1 |
| 2 |
| 4-OM |
| OM |
| 1 |
| 2 |
| 8 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| DB |
| OA |
| BM |
| OM |
| 1 |
| 2 |
| 3 |
| 3 |
| 8 |
| 3 |
2
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 3n |
| PN |
| EF |
| AN |
| AF |
| 2t |
| 8-t |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2t |
| 8-t |
4
| ||
| 8-t |
| 8 |
| 3 |
| 8 |
| 3 |
| BE |
| OA |
| BP |
| OP |
| BE |
| 2 |
| 4-t |
| t |
| 2(4-t) |
| t |
| 3 |
| BM |
| OM |
| 1 |
| 2 |
| 4-OM |
| OM |
| 1 |
| 2 |
| 8 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| DB |
| OA |
| BM |
| OM |
| 1 |
| 2 |
| 3 |
| 3 |
| 8 |
| 3 |
2
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
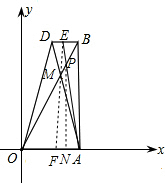
| 3 |
| PN |
| EF |
| AN |
| AF |
| ||||
2
|
2-
| ||
| 2-n |
| t |
| 2n |
| 4-t |
| 2-n |
| 2t |
| 8-t |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2t |
| 8-t |
4
| ||
| 8-t |
| 8 |
| 3 |
| 8 |
| 3 |
| BE |
| OA |
| BP |
| OP |
| BE |
| 2 |
| 4-t |
| t |
| 2(4-t) |
| t |
| 1 |
| 2 |
| 1 |
| 2 |
| 2(4-t) |
| t |
| 3 |
| 4-t |
| t |
| 3 |
2
| ||
| t |
8
| ||||
| t |
| 1 |
| 2 |
| 3 |
| 4-t |
| t |
| 3 |
| 3 |
| 4-t |
| t |
| 3 |
8
| ||
| t |
| 3 |
|
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
|
| ||
| 4-t |
2
| ||
| 4-t |
| ||
| 4-t |
2
| ||
| 4-t |
| 8 |
| 3 |
| 3 |
| ||
| 4-t |
2
| ||
| 4-t |
| 3 |
| tn |
| t-4 |
| 2t |
| t-4 |
| 2t |
| 8-t |
4
| ||
| 8-t |
| 8 |
| 3 |
| 8 |
| 3 |
| 3 |
| ||
| 4-t |
2
| ||
| 4-t |
| 3 |
| tn |
| t-4 |
| 2t |
| t-4 |
| 4t-8 |
| t |
| 4t-8 |
| t |
| 2(4-t) |
| t |
| 1 |
| 2 |
| 3 |
| 4-t |
| t |
| 3 |
| 3 |
| 4-t |
| t |
| 3 |