
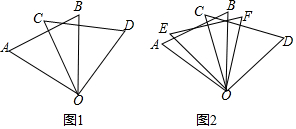
分析 (1)根据等边三角形的性质得到∠AOB=∠COD=60°,根据角的和差即可得到结论;
(2)根据等边三角形的性质得到∠AOB=∠COD=60°,根据角的和差即可得到结论;
(3)根据等边三角形的性质得到∠AOB=∠EOF=60°,根据角的和差即可得到结论.
解答 解:(1)∵△AOB,△COD是等边三角形,
∴∠AOB=∠COD=60°,
∵∠BOC=20°,
∴∠AOD=60°+60°-20°=100°;
故答案为:100;
(2)∵△AOB,△COD是等边三角形,
∴∠AOB=∠COD=60°,
∵∠BOC=x°,
∴∠AOC=∠BOD=60°-x°,
∴∠AOD+∠BOC=60°+60°-x°+x°=120°,
故答案为:120°;
(3)∠AOE,∠COB,∠FOD的和是定值,
理由:∵△AOB,△EOF是等边三角形,
∴∠AOB=∠EOF=60°,
∴∠AOE=∠BOF=60°-∠BOE,
∵∠COD=∠BOC+∠BOF+DOF=∠BOC+∠AOE+∠DOF=60°,
∴∠AOE,∠COB,∠FOD的和是定值.
点评 本题考查了等边三角形的性质,熟练掌握等边三角形的性质是解题的关键.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 直线y=-x+2与X轴、y轴交于A、B两点,C在y轴的负半轴上,且OC=OB.
直线y=-x+2与X轴、y轴交于A、B两点,C在y轴的负半轴上,且OC=OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某公园对一个边长为a(a>1)的正方形花坛进行改造,由于占地需要,正方形花坛南北方向需要缩短1米,使其形状成为长方形.为了使花坛中的绿植面积不变,公园决定将花坛向东侧扩展,使得到的长方形面积和原来正方形的面积相等.
某公园对一个边长为a(a>1)的正方形花坛进行改造,由于占地需要,正方形花坛南北方向需要缩短1米,使其形状成为长方形.为了使花坛中的绿植面积不变,公园决定将花坛向东侧扩展,使得到的长方形面积和原来正方形的面积相等.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com