
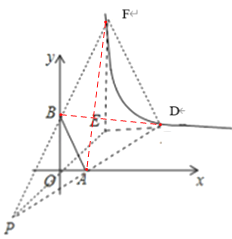
【题目】已知:如图1,点A (1, 0),B(0,2),将点B沿x轴正方向平移3个单位长度得到对应点B′,点B′ 恰在反比例函数y=![]() (x>0)的图象上.
(x>0)的图象上.
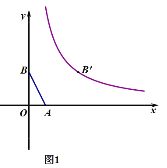
(1)求k的值;
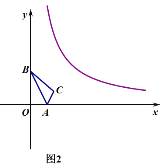
(2)如图2,将△AOB (点O为坐标原点)沿AB翻折得到△ACB,求点C的坐标;
(3)是否存在这样的点P,以P为位似中心,将△AOB放大为原来的两倍后得到△DEF (即△DEF∽△AOB,且相似比为2),使得点D、F恰好在反比例函数y=![]() (x>0) 的图象上?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
(x>0) 的图象上?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
【答案】(1)6;(2)![]() ,
,![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)利用平移规律确定出![]() 的坐标,代入反比例解析式求出
的坐标,代入反比例解析式求出![]() 的值即可;
的值即可;
(2)过C作CM⊥x轴于N,作BM⊥CM与M,证明△ANC∽△CMB,设AN=p,根据比例关系得到方程,求解即可;
(3)![]() 放大为原来的两倍后得到
放大为原来的两倍后得到![]() ,且
,且![]() ,则点
,则点![]() 和
和![]() 一定在反比例函数图象上,设出
一定在反比例函数图象上,设出![]() 与
与![]() 坐标,根据该相似三角形的对应边成比例列出比例式并解答.
坐标,根据该相似三角形的对应边成比例列出比例式并解答.
解:(1)点![]() 沿
沿![]() 轴正方向平移3个单位长度得到对应点
轴正方向平移3个单位长度得到对应点![]() 的坐标是
的坐标是![]() ,
,
代入![]() 得:
得:![]() ;
;
(2)如图,过C做CM⊥x轴于N,作BM⊥CM与M,
∵△AOB沿AB翻折得到△ACB,
∴AC=OA=1,BC=BO=2,∠BCA=∠BOA=90°.
∴∠BCM+∠ACN=90°,
∵∠CAN+∠ACN=90°,
∴∠BCM=∠CAN,
∵∠M=∠ANC=90°,
∴△ANC∽△CMB,
∴![]()
设AN=p,则CM=2p,CN=2-2p,
∴1+p=2(2-2p)
解得![]() ,
,
∴ON=![]() ,CN=
,CN=![]() ,
,
则![]() 的坐标是
的坐标是![]() ,
,![]() ;
;
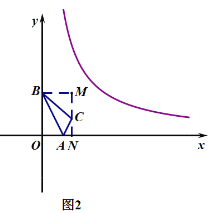
(3)①如图中,![]() 放大为原来的两倍后得到
放大为原来的两倍后得到![]() ,且
,且![]() ,
,
∵OA=1,OB=2
∴EF=4,DE=2,
∵![]() 和
和![]() 在反比例函数图象上,设
在反比例函数图象上,设![]() ,
,
∴![]() ,
,
![]() ,
,
解得![]() 或
或![]() (舍弃),
(舍弃),
经检验m=1是原方程的解,
![]() ,
,![]() ,
,
∴点E坐标为(1,2),
![]() 直线
直线![]() 的解析式为
的解析式为![]()
直线![]() 的解析式为
的解析式为![]() ,
,
由![]() 解得
解得![]() ,
,
![]() ,
,
②连接![]() 、
、![]() ,
,
∵点B坐标为(0,2),点D坐标为(3,2),
∴BD∥x轴,
∵点A坐标为(1,0),点F坐标为(1,6),
∴AF∥y轴,
∴![]() 、
、![]() 的交点
的交点![]() ,
,
![]() 或
或![]() 即为位似中心,(图只是作为参考!
即为位似中心,(图只是作为参考!![]()
综上所述,![]() 坐标为
坐标为![]() 或
或![]() .
.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
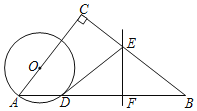
【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=3,BC=4,OA=1,求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点A和点B(3,0),与
轴交于点A和点B(3,0),与![]() 轴交于点C(0,3).
轴交于点C(0,3).

(1)求抛物线的解析式;
(2)若点M是抛物线在![]() 轴下方上的动点,过点M作MN//
轴下方上的动点,过点M作MN//![]() 轴交直线BC于点N,求线段MN的最大值;
轴交直线BC于点N,求线段MN的最大值;
(3)在(2)的条件下,当MN取最大值时,在抛物线的对称轴![]() 上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
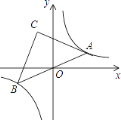
【题目】如图,在反比例函数y= ![]() 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= ![]() 的图象上运动,若tan∠CAB=2,则k的值为( )
的图象上运动,若tan∠CAB=2,则k的值为( )
A. ﹣3 B. ﹣6 C. ﹣9 D. ﹣12
查看答案和解析>>
科目:初中数学 来源: 题型:
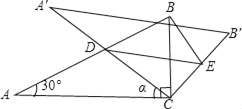
【题目】如图,将含30°角的直角三角板ABC(∠A=30°)绕其直角顶点C顺时针旋转α角(0°<α<90°),得到Rt△A′B′C,A′C与AB交于点D,过点D作DE∥A′B′交CB′于点E,连接BE.易知,在旋转过程中,△BDE为直角三角形.设BC=1,AD=x,△BDE的面积为S.
(1)当α=30°时,求x的值.
(2)求S与x的函数关系式,并写出x的取值范围;
(3)以点E为圆心,BE为半径作⊙E,当S=![]() 时,判断⊙E与A′C的位置关系,并求相应的tanα值.
时,判断⊙E与A′C的位置关系,并求相应的tanα值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有红、黑两种颜色的球共60只,这些球除颜色外其余完全相同.为了估计红球和黑球的个数,七(2)班的数学学习小组做了摸球实验.他们将球搅匀后,从盒子里随机摸出一个球记下颜色,再把球放回盒子中,多次重复上述过程,得到表中的一组统计数据:
摸球的次数n | 50 | 100 | 300 | 500 | 800 | 1000 |
摸到红球的次数m | 14 | 33 | 95 | 155 | 241 | 298 |
摸到红球的频率 | 0.28 | 0.33 | 0.317 | 0.31 | 0.301 | 0.298 |
请估计:当次数n足够大时,摸到红球的频率将会接近_____.(精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,AB=AC, ∠BAC <60°,将线段 AB 绕点 A逆时针旋转 60°得到点 D, 点 E 与点 D 关于直线 BC 对称,连接 CD,CE,DE.
(1)依题意补全图形;
(2)判断△CDE 的形状,并证明;
(3)请问在直线CE上是否存在点 P,使得 PA - PB =CD 成立?若存在,请用文字描述出点 P 的准确位置,并画图证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
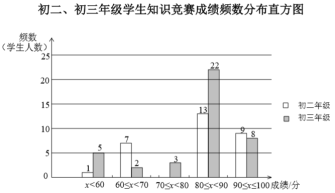
【题目】某学校初二和初三两个年级各有600名同学,为了科普卫生防疫知识,学校组织了一次在线知识竞赛,小宇分别从初二、初三两个年级随机抽取了40名同学的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
![]() .初二、初三年级学生知识竞赛成绩不完整的频数分布直方图如下(数据分成5组:
.初二、初三年级学生知识竞赛成绩不完整的频数分布直方图如下(数据分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
![]() .初二年级学生知识竞赛成绩在
.初二年级学生知识竞赛成绩在![]() 这一组的数据如下:
这一组的数据如下:
80 80 81 83 83 84 84 85 86 87 88 89 89
![]() .初二、初三学生知识竞赛成绩的平均数、中位数、方差如下:
.初二、初三学生知识竞赛成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
初二年级 | 80.8 |
| 96.9 |
初三年级 | 80.6 | 86 | 153.3 |
根据以上信息,回答下列问题:
(1)补全上面的知识竞赛成绩频数分布直方图;
(2)写出表中![]() 的值;
的值;
(3)![]() 同学看到上述的信息后,说自己的成绩能在本年级排在前40%,
同学看到上述的信息后,说自己的成绩能在本年级排在前40%,![]() 同学看到
同学看到![]() 同学的成绩后说:“很遗憾,你的成绩在我们年级进不了前50%”.请判断
同学的成绩后说:“很遗憾,你的成绩在我们年级进不了前50%”.请判断![]() 同学是________(填“初二”或“初三”)年级的学,你判断的理由是________.
同学是________(填“初二”或“初三”)年级的学,你判断的理由是________.
(4)若成绩在85分及以上为优秀,请估计初二年级竞赛成绩优秀的人数为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣4、3、5这三个数中,随机抽取一个数,记为a,那么,使关于x的方程x2+4x+a=0有解,且使关于x的一次函数y=2x+a的图象与x轴、y轴围成的三角形面积恰好为4的概率_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com