
【题目】已知抛物线 y=a(x﹣2)![]() +1 经过点 P(1,﹣3)
+1 经过点 P(1,﹣3)
(1)求 a 的值;
(2)若点 A(m,y![]() )、B(n ,y
)、B(n ,y![]() )(m<n<2)都在该抛物线上,试比较 y
)(m<n<2)都在该抛物线上,试比较 y![]() 与y
与y![]() 的大小.
的大小.
科目:初中数学 来源: 题型:
【题目】由甲、乙两个工程队承包某校校园绿化工程,甲、乙两队单独完成这项工程所需时间比是3︰2,两队合做6天可以完成.
(1)求两队单独完成此项工程各需多少天?
(2)此项工程由甲、乙两队合做6天完成任务后,学校付给他们20000元报酬,若
按各自完成的工程量分配这笔钱,问甲、乙两队各得到多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
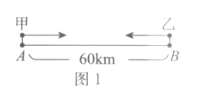
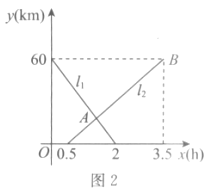
【题目】如图1所示,A,B两地相距60km,甲、乙分别从A,B两地出发,相向而行,图2中的![]() ,
,![]() 分别表示甲、乙离B地的距离y(km)与甲出发后所用的时间x(h)的函数关系.以下结论正确的是( )
分别表示甲、乙离B地的距离y(km)与甲出发后所用的时间x(h)的函数关系.以下结论正确的是( )
A.甲的速度为20km/h
B.甲和乙同时出发
C.甲出发1.4h时与乙相遇
D.乙出发3.5h时到达A地
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC 中,AB=AC,过其中一个顶点的直线可以把这个三角形分成另外两个等腰三角形,则∠BAC( )
A. 36°,90°,![]() , 108°B. 36°,72°,
, 108°B. 36°,72°,![]() ,90°
,90°
C. 90°,72°,108°,![]() D. 36°,90°,108°,
D. 36°,90°,108°,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2014年巴西世界杯足球赛前夕,某体育用品店购进一批单价为40元的球服,如果按单价60元销售,那么一个月内可售出240套.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套.设销售单价为x(x≥60)元,销售量为y套.
(1)求出y与x的函数关系式.
(2)当销售单价为多少元时,月销售额为14000元?
(3)当销售单价为多少元时,才能在一个月内获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
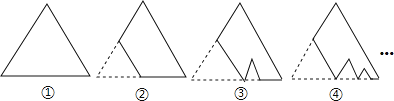
【题目】如图,图①是一块边长为1,周长记为P1的等边三角形纸板,沿图①的底边剪去一块边长的![]() 的等边三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的
的等边三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的![]() )后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则Pn-Pn-1=_________
)后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则Pn-Pn-1=_________
查看答案和解析>>
科目:初中数学 来源: 题型:
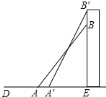
【题目】一根竹竿长![]() 米,先像
米,先像![]() 靠墙放置,与水平夹角为
靠墙放置,与水平夹角为![]() ,为了减少占地空间,现将竹竿像
,为了减少占地空间,现将竹竿像![]() 放置,与水平夹角为
放置,与水平夹角为![]() ,则竹竿让出多少水平空间( )
,则竹竿让出多少水平空间( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并按要求解答.
(模型建立)如图①,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.求证:△BEC≌△CDA.
(模型应用)
应用1:如图②,在四边形ABCD中,∠ADC=90°,AD=6,CD=8,BC=10,AB2=200.求线段BD的长.
应用2:如图 ③,在平面直角坐标系中,纸片△OPQ为等腰直角三角形,QO=QP,P(4,m),点Q始终在直线OP的上方.
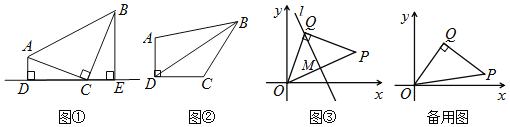
(1)折叠纸片,使得点P与点O重合,折痕所在的直线l过点Q且与线段OP交于点M,当m=2时,求Q点的坐标和直线l与x轴的交点坐标;
(2)若无论m取何值,点Q总在某条确定的直线上,请直接写出这条直线的解析式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,小明和父母一起开车到距家200千米的景点旅游.出发前,汽车油箱内储油45升;当行驶150千米时,发现油箱剩余油量为30升.
(1)已知油箱内余油量y(升)是行驶路程x(千米)的一次函数,求y与x的函数关系式;
(2)当油箱中余油量少于3升时,汽车将自动报警.如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com