
| A. | b≤-3或b>0 | B. | b=-2或b>0 | C. | b=-3或b>0 | D. | b=-2 |
分析 由于方程含有绝对值,因此需要分两种情况去掉绝对值号,然后根据一元二次方程的根情况进行讨论.
解答 解:当x≥4时,
原方程化为:x2-8x+(b-3)(x-4)+16-3b=0,
化简为:x2+(b-11)x+28-7b=0,
此时,△=(b-11)2-4(28-7b)=(b+3)2≥0,
∴此时方程的解为:x1=7,x2=4-b,
当x<4时,
原方程化为:x2-8x-(b-3)(x-4)+16-3b=0,
化简为:x2-(b+5)x+b+4=0,
此时,△=(b+5)2-4(b+4)=(b+3)2≥0,
∴此时方程的解为:x3=1,x4=b+4,
当b=-3时,
此时x1=x2=7,x3=x4=1,
此情况满足题意.
当$\left\{\begin{array}{l}{4-b<4}\\{b+4≥4}\end{array}\right.$时,
此时:b>0,
综上所述,b=-3且b>0,
故选(C)
点评 本题考查根的判别式,涉及一元二次方程的解,分类讨论的思想,属于中等题型.


科目:初中数学 来源: 题型:填空题
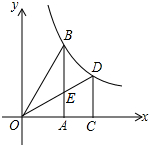 如图,B、D是反比例函数y=$\frac{k}{x}$图象上两点,过B,D作x轴的垂线,垂足分别为A,C,连接OD交AB于点E,若∠ABO=30°,OD是∠BOA的平分线,四边形ACDE的面积为2,则k=6.
如图,B、D是反比例函数y=$\frac{k}{x}$图象上两点,过B,D作x轴的垂线,垂足分别为A,C,连接OD交AB于点E,若∠ABO=30°,OD是∠BOA的平分线,四边形ACDE的面积为2,则k=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某宾馆在重新装修后,考虑在大厅内的主楼梯上铺设地毯,已知主楼梯宽3米,其剖面如图所示,请你计算一下:
某宾馆在重新装修后,考虑在大厅内的主楼梯上铺设地毯,已知主楼梯宽3米,其剖面如图所示,请你计算一下:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图△ABC中,∠C=90°,AD平分∠BAC,若AB=9,CD=2,则△ABD的面积是( )
如图△ABC中,∠C=90°,AD平分∠BAC,若AB=9,CD=2,则△ABD的面积是( )| A. | $\frac{9}{2}$ | B. | 9 | C. | 18 | D. | $\frac{9}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com