
【题目】已知,点E、F分别在直线AB,CD上,点P在AB、CD之间,连结EP、FP,如图1,过FP上的点G作GH∥EP,交CD于点H,且∠1=∠2.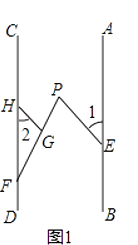
(1)求证:AB∥CD;
(2)如图2,将射线FC沿FP折叠,交PE于点J,若JK平分∠EJF,且JK∥AB,则∠BEP与∠EPF之间有何数量关系,并证明你的结论;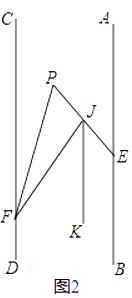
(3)如图3,将射线FC沿FP折叠,将射线EA沿EP折叠,折叠后的两射线交于点M,当EM⊥FM时,求∠EPF的度数.
【答案】
(1)
解:延长FP交AB于点Q,如图1,
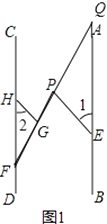
∵PE∥HG,
∴∠GPE=∠HGP,
∵∠GPE=∠1+∠PQE,∠HGP=∠2+∠HFG,
∵∠1=∠2,
∴∠PQE=∠HFG,
∴AB∥CD
(2)
解:延长FP交CD于点Q,如图2,
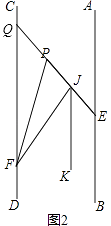
∠EPF+ ![]() ∠BEP=270°,理由如下:
∠BEP=270°,理由如下:
∵AB∥CD,
∴∠BEP+∠FQP=180°,
∵将射线FC沿FP折叠,
∴∠QFP=∠PFJ,
∵JK∥AB,
∴JK∥CD,
∴∠FJK=2∠CFP,
∵∠EPF=∠EQF+∠QFP,
∴∠EPF=180°﹣∠BEP+∠QFP,
∵JK平分∠EJF,
∴∠FJK=∠KJE,
∵JK∥CD,
∴∠KJE=∠FQP,
∴∠EPF=180°﹣∠BEP+ ![]() ∠FJK,
∠FJK,
∴∠EPF=180°﹣∠BEP+ ![]() ,
,
∴∠EPF+ ![]() ∠BEP=270°
∠BEP=270°
(3)
解:延长FP交AB于点Q,如图3,
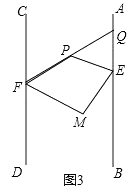
∵AB∥CD,
∴∠CFQ=∠PQE,
∵将射线FC沿FP折叠,将射线EA沿EP折叠,
∴∠CFP=∠PFM,∠MEP=∠PEQ,
∵∠FPE=∠PQE+∠PEQ,
在四边形FPEM中,
∠PFM+∠MEP+∠FPE=360°﹣90°=270°,
可得:2∠FPE=270°,
∴∠FPE=135°
【解析】(1)延长FP交AB于点Q,根据三角形的外角性质和平行线性质证明即可;(2)延长FP交CD于点Q,根据折叠和平行线的性质解答即可;(3)延长FP交AB于点Q,根据折叠和四边形的内角和进行分析解答.
【考点精析】本题主要考查了平行线的判定与性质和翻折变换(折叠问题)的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠BAD的角平分线与边BC交于点E,∠ADC的角平分线交直线AE于点O.
(1)若点O在四边形ABCD的内部,
如图1,若AD∥BC,∠B=40°,∠C=70°,则∠DOE=°;
(2)如图2,试探索∠B、∠C、∠DOE之间的数量关系,并将你的探索过程写下来.
(3)如图3,若点O在四边形ABCD的外部,请你直接写出∠B、∠C、∠DOE之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力。如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点 C为一海港,且点 C与直线 AB上两点A,B的距离分别为300km和400km,又 AB=500km,以台风中心为圆心周围250km以内为受影响区域。

(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20km/h,台风影响该海港持续的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是重叠的两个直角三角形,将三角形ABC沿AB方向平移2cm后,得到三角形DEF,若CH=2cm,EF=4cm,则图中阴影部分面积为cm2 . 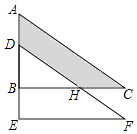
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.
月信息消费额分组统计表
组别 | 消费额(元) |
A | 10≤x<100 |
B | 100≤x<200 |
C | 20≤x<300 |
D | 300≤x<400 |
E | x≥400 |
请结合图表中相关数据解答下列问题:
(1)这次接受调查的有 户;
(2)在扇形统计图中,“E”所对应的圆心角的度数是 ;
(3)请你补全频数直方图;
(4)若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中的系数等等. 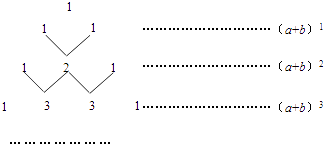
(1)根据上面的规律,则(a+b)5的展开式= .
(2)利用上面的规律计算:25﹣5×24+10×23﹣10×22+5×2﹣1= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com