
【题目】如图,已知在△ABC中,AB=AC=12cm,BC=9cm,D为AB中点,设点P在线段BC上以3cm/s的速度由B点向C点运动,点Q在线段CA上由C点向A点运动.

(1)若Q点运动的速度与P点相同,且点P、Q同时出发,经过1秒钟后△BPD与△CQP是否全等,并说明理由;
(2)若点P、Q同时出发,但运动的速度不相同,当Q点的运动速度为多少时,能在运动过程中有△BPD与△CQP全等?
【答案】(1)全等,理由见解析;(2)当Q点运动速度为![]() cm/s时全等,理由见解析
cm/s时全等,理由见解析
【解析】
(1)由运动时间易得BP=CQ=3cm,所以PC=6cm,再由条件可得∠B=∠C,利用SAS即可判定全等;
(2)由速度不同可知BP≠CQ,要使△BPD≌△CPQ,只能BP=CP=4.5,即可求出运动时间,此时CQ=BD=6,用路程除以时间即可得速度.
(1)∵t=1s
∴BP=CQ=3cm
∵AB=12,D为AB中点,
∴BD=6cm
又∵PC=BCBP=93=6cm
∴PC=BD
∵AB=AC,
∴∠B=∠C,
在△BPD与△CQP中,
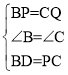
∴△BPD≌△CQP(SAS)
(2)∵VP≠VQ
∴BP≠CQ,
又∵∠B=∠C,
要使△BPD≌△CPQ,只能BP=CP=4.5,
∵△BPD≌△CPQ,
∴CQ=BD=6.
∴点P的运动时间![]() s,
s,
此时VQ=![]() cm/s.
cm/s.


科目:初中数学 来源: 题型:
【题目】如图,边长为![]() 的菱形
的菱形![]() 中,
中,![]() ,以对角线
,以对角线![]() 为边作第
为边作第![]() 个菱形
个菱形![]() ,使
,使![]() .连结
.连结![]() ,再以
,再以![]() 为边作第
为边作第![]() 个菱形
个菱形![]() 使
使![]() …,则第
…,则第![]() 个菱形的边长是________,按此规律所作第
个菱形的边长是________,按此规律所作第![]() 个菱形的边长是________.
个菱形的边长是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店销售一种品牌的羽绒服,平均每天可以销售![]() 件,每件盈利
件,每件盈利![]() 元,为了扩大销售,减少库存,商店决定降价销售,经调查,每件羽绒服每降价
元,为了扩大销售,减少库存,商店决定降价销售,经调查,每件羽绒服每降价![]() 元时,平均每天就多卖出
元时,平均每天就多卖出![]() 件,但是综合多方因素,降价后,每件盈利不能低于原来每件利润的一半.
件,但是综合多方因素,降价后,每件盈利不能低于原来每件利润的一半.
![]() 若商场要求该羽绒服每天盈利
若商场要求该羽绒服每天盈利![]() 元,每件羽绒服应降价多少元?
元,每件羽绒服应降价多少元?
![]() 试说明每件羽绒服降价多少元时,盈利最多?
试说明每件羽绒服降价多少元时,盈利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由正比例函数![]() 沿
沿![]() 轴的正方向平移4个单位而成的一次函数
轴的正方向平移4个单位而成的一次函数![]()
的图像与反比例函数![]() (
(![]() )在第一象限的图像交于A(1,n)和B两点.
)在第一象限的图像交于A(1,n)和B两点.
(1)求一次函数![]() 和反比例函数的解析式;
和反比例函数的解析式;
(2)求△ABO的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为56和32,则△EDF的面积为()

A.10B.11C.12D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:

(1)∠BAE的度数;
(2)∠DAE的度数;
(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B-∠C=40°,也能得出∠DAE的度数?若能,请你写出求解过程;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=BC, BD⊥AC,垂足为D,过点D作DE⊥DF,交AB于点E,交BC于点F.

(1)求证:△DBE≌△DCF;
(2)连接EF,若AE=4,FC=3;求
①EF的长;
②四边形BFDE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com