
【题目】某市射击队打算从君君、标标两名运动员中选拔一人参加省射击比赛,射击队对两人的射击技能进行了测评.在相同的条件下,两人各打靶5次,成绩统计如下:
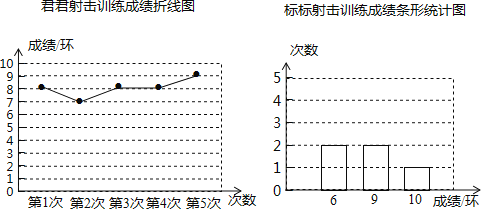
(1)填写下表:
平均数(环) | 中位数(环) | 方差(环2) | |
君君 |
| 8 | 0.4 |
标标 | 8 |
|
|
(2)根据以上信息,若选派一名队员参赛,你认为应选哪名队员,并说明理由.
(3)如果标标再射击1次,命中8环,那么他射击成绩的方差会 .(填“变大”“变小”或“不变”)
【答案】(1)8,9,2.8;(2)选君君;理由见解析;(3)变小.
【解析】
(1)根据平均数、中位数以及方差的定义即可得出答案;
(2)比较平均数和方差,在平均数相等的情况下,选择方差小的,即可得出答案;
(3)根据方差的定义计算即可得出答案.
解:(1)君君的平均数=(8+7+8+8+9)÷5=8
标标的中位数为:9
标标的方差=![]()
填写下表:
平均数(环) | 中位数(环) | 方差(环2) | |
君君 | 8 | 8 | 0.4 |
标标 | 8 | 9 | 2.8 |
故答案为:8,9,2.8;
(2)选君君,理由:∵两人的平均值相等,君君的方差较小,成绩更稳定,
∴选君君;
(3)因为再射一次,标标的方差=![]() ,
,
所以如果标标再射击1次,命中8环,那么标标的射击成绩的方差变小.
故答案为:变小.


科目:初中数学 来源: 题型:
【题目】(本题满分8分)在一个不透明的袋中装有3 个完全相同的小球,上面分别标号为1、2、3,从中随机摸出两个小球,并用球上的数字组成一个两位数.
(1)求组成的两位数是奇数的概率;
(2)小明和小华做游戏,规则是:若组成的两位数是4的倍数,小明得3分,否则小华得3分,你认为该游戏公平吗?说明理由;若不公平,请修改游戏规则,使游戏公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中以AB为直径作⊙O,分别交边AC、BC于D、E,过D作DF⊥BC于F,且D为弧AE的中点.
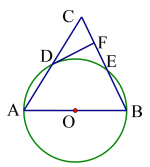
(1)求证:DF为⊙O的切线;
(2)若![]() 且AD=
且AD=![]() 时,求⊙O的半径
时,求⊙O的半径![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C地在A地的正东方向,因有大山阻隔.由A地到C地需绕行B地,已知B地位于A地北偏东67°方向,距离A地130km,C地位于B地南偏东30°方向.若打通穿山隧道.建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.73)
≈1.73)
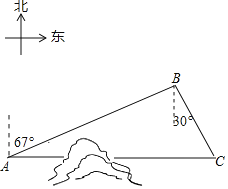
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0,a、b、c为常数)上部分点的横坐标x,纵坐标y的对应值如下表:
x | …… | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | …… |
y | …… |
| 4 |
| 4 | m | 0 | …… |
则下列结论中:①抛物线的对称轴为直线x=﹣1;②m=![]() ;③当﹣4<x<2时,y<0;④方程ax2+bx+c﹣4=0的两根分别是x1=﹣2,x2=0,其中正确的个数有( )
;③当﹣4<x<2时,y<0;④方程ax2+bx+c﹣4=0的两根分别是x1=﹣2,x2=0,其中正确的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象与y轴交于点A(0,4),与x轴交于点B,C,点C坐标为(8,0),连接AB,AC.
的图象与y轴交于点A(0,4),与x轴交于点B,C,点C坐标为(8,0),连接AB,AC.

(1)请直接写出二次函数![]() 的解析式.
的解析式.
(2)判断△ABC的形状,并说明理由.
(3)若点N在x轴上运动,当以点A,N,C为顶点的三角形是等腰三角形时,请写出此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在BC边上,AE与BD交于点F,∠BAE=∠ADB.
(1)图中与△ABF相似的三角形(不包括△ABF本身)共有_____个.
(2)若BE=2,AD=5.求:AB的长.
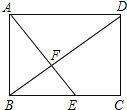
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(-1,0),B(0,2),点C在x轴上,且∠ABC=90°.
(1)求点C的坐标;
(2)求经过A,B,C三点的抛物线的表达式;
(3)在(2)中的抛物线上是否存在点P,使∠PAC=∠BCO?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com