
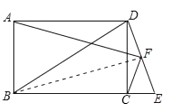
【题目】已知,矩形ABCD中,延长BC至E,连接DE,F为DE的中点,连结AF、CF且AF⊥CF.
求证:(1)∠ADF=∠BCF;
(2)BD=AD+CE.

【答案】见解析
【解析】
(1)根据F为中点得到CF=DF=EF,再得到∠CDF=∠DCF,再利用矩形的性质即可求解;
(2)先根据全等三角形的判定与性质得到△BDE为等腰三角形,再根据线段之间的关系即可证明.
(1)在矩形ABCD中,
∵AD=BC,∠ADC=∠BCD=90°,
∴∠DCE=90°,
在Rt△DCE中,
∵F为DE中点,
∴DF=CF,
∴∠CDF=∠DCF,
∴∠ADC+∠CDF=∠BCD+∠DCF,
即∠ADF=∠BCF;
(2)连接BF,
在△AFD和△BFC中
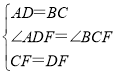 ,
,
∴△ADF≌△BCF,
∴∠AFD=∠BFC,
∵AF⊥CF,
∴∠AFD+∠AFB =∠BFC+∠AFB=90°
∴BF⊥DE,
∵F为DE中点,
在△BDF和△BEF中
 ,
,
∴△ADF≌△BCF,
∴BD=BE
∵BE=BC+CE
∴BD=BC+CE= AD+CE.
故BD=AD+CE.


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2).
(1)直接写出点A1,B1,C1的坐标.
(2)在图中画出△A1B1C1.
(3)连接AA1,求△AOA1的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:小明遇到这样一个问题:已知:在△ABC中,AB,BC,AC三边的长分别为![]() ,求△ABC的面积.小明是这样解决问题的:如图①所示,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),从而借助网格就能计算出△ABC的面积.他把这种解决问题的方法称为构图法.请回答:
,求△ABC的面积.小明是这样解决问题的:如图①所示,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),从而借助网格就能计算出△ABC的面积.他把这种解决问题的方法称为构图法.请回答:

(1)图1中△ABC的面积为 ;
参考小明解决问题的方法,完成下列问题:
(2)图2是一个6×6的正方形网格(每个小正方形的边长为1).
①利用构图法在答卷的图2中画出三边长分别为![]() 、2
、2![]() 、
、![]() 的格点△DEF;
的格点△DEF;
②计算△DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=60°,AB=2,E是DC边上一个动点,F是AB边上一点,∠AEF=30°.设DE=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图所示,则这条线段可能是图中的( ).

A. 线段EC B. 线段AE C. 线段EF D. 线段BF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线l1:y=2x+3与直线l2:y=kx+b的交点A在y轴上,直线l3:y=x与直线l1相交于点B与直线l2相交于点C(1,1).
(1)求直线l2的解析式和B点的坐标;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 直线![]() 与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点, 点P为OA上一动点, 当PC+PD最小时, 点P的坐标为( )
与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点, 点P为OA上一动点, 当PC+PD最小时, 点P的坐标为( )

A.(-4,0)B.(-1,0)C.(-2,0)D.(-3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乳品公司向某地运输一批牛奶,由铁路运输每千克需运费0.60元,由公路运输,每千克需运费0.30元,另需补助600元
(1)设该公司运输的这批牛奶为x千克,选择铁路运输时,所需运费为y1元,选择公路运输时,所需运费为y2元,请分别写出y1、y2与x之间的关系式;
(2)若公司只支出运费1500元,则选用哪种运输方式运送的牛奶多?若公司运送1500千克牛奶,则选用哪种运输方式所需费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条河的两岸BC与DE互相平行,两岸各有一排景观灯(图中黑点代表景观灯),每排相邻两景观灯的间隔都是10 m,在与河岸DE的距离为16 m的A处(AD⊥DE)看对岸BC,看到对岸BC上的两个景观灯的灯杆恰好被河岸DE上两个景观灯的灯杆遮住.河岸DE上的两个景观灯之间有1个景观灯,河岸BC上被遮住的两个景观灯之间有4个景观灯,求这条河的宽度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蔬菜基地种植某种蔬菜,由市场行情分析知,1月份至6月份这种蔬菜的上市时间![]() (月份)与市场售价
(月份)与市场售价![]() (元/千克)的关系如下表:
(元/千克)的关系如下表:
上市时间 | 1 | 2 | 3 | 4 | 5 | 6 |
市场售价 | 10.5 | 9 | 7.5 | 6 | 4.5 | 3 |
这种蔬菜每千克的种植成本![]() (元/千克)与上市时间
(元/千克)与上市时间![]() (月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).
(月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).
(1)写出上表中表示的市场售价![]() (元/千克)关于上市时间
(元/千克)关于上市时间![]() (月份)的函数关系式;
(月份)的函数关系式;
(2)若图中抛物线过![]() 点,写出抛物线对应的函数关系式;
点,写出抛物线对应的函数关系式;
(3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com