
(1)动手操作:
如图①,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点 处,折痕为EF,若∠ABE=20°,那么∠
处,折痕为EF,若∠ABE=20°,那么∠ 的度数为____________.
的度数为____________.

(2)观察发现:
小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图②);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图③).小明认为△AEF是等腰三角形,你同意吗?请说 明理由.
明理由.

(3)实践与运用:
将矩形纸片ABCD 按如下步骤操作:将纸片对折得折痕EF,折痕与AD边交于点E,与BC边交于点F;将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠,使点A、点D都与点F重合,展开纸片,此时恰好有MP=MN=PQ(如图④),求∠MNF的大小.

125°;同意;60°.
详解:(1)∵在Rt△ABE中,∠ABE=20°,
∴∠AEB=70°,∴∠BED=110°,
根据折叠重合的角相等,得∠BEF=∠DEF=55°.
∵AD∥BC,∴∠EFC=125°,
再根据折叠的性质得到∠ =∠EFC=125°.
=∠EFC=125°.
(2)同意.如图,设AD与EF交于点G.
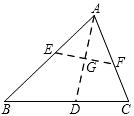
由折叠知,AD平分∠BAC,所以∠BAD=∠CAD.
由折叠知,∠AGE=∠DGE=90°,
∴∠AGE=∠AGF=90°,∴∠AEF=∠AFE,∴AE=AF,
即△AEF为等腰三角形.
(3)由题意得出: ∠NMF=∠AMN=∠MNF,
∴MF=NF,由对称性可知,MF=PF,∴NF=PF,
而由题意得出:MP=MN,MF=MF,
在△MNF和△MPF中, ,
,
∴△MNF≌△MPF(SSS),
∴∠PMF=∠NMF,而∠PMF+∠NMF+∠MNF=180°,
即3∠MNF=180°,∴∠MNF=60°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
如图8-1,在正方形ABCD和正方形BEFG中,点A,B,E在同一条直线上,连接DF,且P是线段DF的中点,连接PG,PC.
(1)如图8-1中,PG与PC的位置关系是 ,数量关系是 ;(4分)
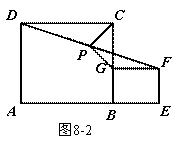
(2) 如图8-2将条件“正方形ABCD和正方形BEFG”改为“矩形ABCD和矩形BEFG”其它条件不变,求证:PG=PC;(4分)

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知△ABC中,∠BAC=12 0°,分别作AC,AB边的垂直平分线PM,PN交于点P,分别交BC于点E和点F.则
0°,分别作AC,AB边的垂直平分线PM,PN交于点P,分别交BC于点E和点F.则 以下各说法中:
以下各说法中:
①∠P=60°,②∠EAF=60°,③点P到点B和点C的距离相等,④PE=PF.
正确的 说法是______________.(填序号)
说法是______________.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC中,∠BAC=60°,∠ABC、∠ACB的平分线交于E,D是AE延长线上一点,且∠BDC=120°.下列结论:①∠BEC=120°;②DB=DE;③∠DBE=∠DCE.其中正确结论的个数为( )
A.0 B.1 C.2 D.3

查看答案和解析>>
科目:初中数学 来源: 题型:
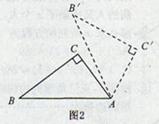
如图2,Rt△ABC中,∠C=90°,AC=3,BC=4,若以A为旋转中心,将其按顺时针方向旋转60°到△AB'C'位置,则B点经过的路线长为( )
A.π B.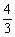 π C.
π C. π D.
π D. π
π
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点
F,且AB=DE。(1)求证:BD=BC;(2)若BD=8cm,求AC的长。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com