
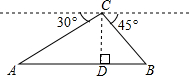
 如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度为200米,点A、B、C在同一直线上,则AB两点间的距离是200($\sqrt{3}$+1)米(结果保留根号).
如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度为200米,点A、B、C在同一直线上,则AB两点间的距离是200($\sqrt{3}$+1)米(结果保留根号). 分析 先根据从热气球C处测得地面A、B两点的俯角分别为30°、45°可求出∠BCD与∠ACD的度数,再由直角三角形的性质求出AD与BD的长,根据AB=AD+BD即可得出结论.
解答  解:∵从热气球C处测得地面A、B两点的俯角分别为30°、45°,
解:∵从热气球C处测得地面A、B两点的俯角分别为30°、45°,
∴∠BCD=90°-45°=45°,∠ACD=90°-30°=60°,
∵CD⊥AB,CD=200m,
∴△BCD是等腰直角三角形,
∴BD=CD=200m,
在Rt△ACD中,CD=200m,∠ACD=60°,
∴AD=CD•tan60°=200×$\sqrt{3}$=200$\sqrt{3}$m,
∴AB=AD+BD=200$\sqrt{3}$+200=200($\sqrt{3}$+1)m.
故答案为:200($\sqrt{3}$+1).
点评 本题考查的是解直角三角形的应用-仰角俯角问题,熟知锐角三角函数的定义是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
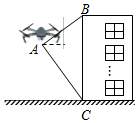 台州湾循环经济产业集聚区正在投资建设无人机小镇,无人机已运用于很多行业.一测绘无人机从A处测得某建筑物顶部B的仰角为37°,底部C的俯角为60°,此时无人机与建筑物水平距离为30米,建筑物的高度BC约为多少米?
台州湾循环经济产业集聚区正在投资建设无人机小镇,无人机已运用于很多行业.一测绘无人机从A处测得某建筑物顶部B的仰角为37°,底部C的俯角为60°,此时无人机与建筑物水平距离为30米,建筑物的高度BC约为多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
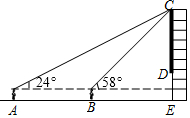 如图是某市中心一家大型购物商城墙面上的电子屏幕,好学的小希想利用所学的知识测量电子屏幕上下端之间的高度,于是她站在屏幕正前方的点A处,测得电子屏幕上端C处的仰角为24°,接着他正对电子屏幕方向前进7m到达点B处,又测得电子屏幕上端C处的仰角为58°,已知图中所有点均在同一平面内,小希的眼睛始终距离地面1.60m,CE⊥AE,DE=3m,请你根据以上测量数据,求该电子屏幕上下端之间的高度CD.(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°≈0.45,sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,结果精确到0.1m)
如图是某市中心一家大型购物商城墙面上的电子屏幕,好学的小希想利用所学的知识测量电子屏幕上下端之间的高度,于是她站在屏幕正前方的点A处,测得电子屏幕上端C处的仰角为24°,接着他正对电子屏幕方向前进7m到达点B处,又测得电子屏幕上端C处的仰角为58°,已知图中所有点均在同一平面内,小希的眼睛始终距离地面1.60m,CE⊥AE,DE=3m,请你根据以上测量数据,求该电子屏幕上下端之间的高度CD.(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°≈0.45,sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,结果精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3<x≤4 | B. | x≤4 | C. | x>3 | D. | 2≤x<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年龄 | 26 | 42 | 57 |
| 健康指数 | 97 | 79 | 72 |
| 年龄 | 23 | 25 | 26 | 32 | 33 | 37 | 39 | 42 | 48 | 52 |
| 健康指数 | 93 | 89 | 90 | 83 | 79 | 75 | 80 | 69 | 68 | 60 |
| 年龄 | 22 | 29 | 31 | 36 | 39 | 40 | 43 | 46 | 51 | 55 |
| 健康指数 | 94 | 90 | 88 | 85 | 82 | 78 | 72 | 76 | 62 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3×104千米/秒 | B. | 3×105千米/秒 | C. | 3×106千米/秒 | D. | 30×104千米/秒 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com