
【题目】如图1,菱形ABCD中,∠A=60°,点P从A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止,点Q从A与P同时出发,沿边AD匀速运动到D终止,设点P运动的时间为t(s).△APQ的面积S(cm2)与t(s)之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出.
(1)求点Q运动的速度;
(2)求图2中线段FG的函数关系式;
(3)问:是否存在这样的t,使PQ将菱形ABCD的面积恰好分成1:5的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
【答案】
(1)
解:由题意,可知题图2中点E表示点P运动至点B时的情形,所用时间为3s,则菱形的边长AB=2×3=6cm.
此时如答图1所示:

AQ边上的高h=ABsin60°=6× ![]() =
= ![]() cm,
cm,
S=S△APQ= ![]() AQh=
AQh= ![]() AQ×
AQ× ![]() =
= ![]() ,解得AQ=3cm,
,解得AQ=3cm,
∴点Q的运动速度为:3÷3=1cm/s.
(2)
解:由题意,可知题图2中FG段表示点P在线段CD上运动时的情形.如答图2所示:

点Q运动至点D所需时间为:6÷1=6s,点P运动至点C所需时间为12÷2=6s,至终点D所需时间为18÷2=9s.
因此在FG段内,点Q运动至点D停止运动,点P在线段CD上继续运动,且时间t的取值范围为:6≤t≤9.
过点P作PE⊥AD交AD的延长线于点E,则PE=PDsin60°=(18﹣2t)× ![]() =
= ![]() t+
t+ ![]() .
.
S=S△APQ= ![]() ADPE=
ADPE= ![]() ×6×(
×6×( ![]() t+
t+ ![]() )=
)= ![]() t+
t+ ![]() ,
,
∴FG段的函数表达式为:S= ![]() t+
t+ ![]() (6≤t≤9).
(6≤t≤9).
(3)
解:菱形ABCD的面积为:6×6×sin60°= ![]() .
.
当点P在AB上运动时,PQ将菱形ABCD分成△APQ和五边形PBCDQ两部分,如答图3所示.
此时△APQ的面积S= ![]() AQAPsin60°=
AQAPsin60°= ![]() t2t×
t2t× ![]() =
= ![]() t2,
t2,
根据题意,得 ![]() t2=
t2= ![]() ×
× ![]() ,
,
解得t= ![]() s(舍去负值);
s(舍去负值);

当点P在BC上运动时,PQ将菱形分为梯形ABPQ和梯形PCDQ两部分,如答图4所示.
此时,有S梯形ABPQ= ![]() S菱形ABCD,即
S菱形ABCD,即 ![]() (2t﹣6+t)×6×
(2t﹣6+t)×6× ![]() =
= ![]() ×
× ![]() ,
,
解得t= ![]() s.
s.
∴存在t= ![]() 和t=
和t= ![]() ,使PQ将菱形ABCD的面积恰好分成1:5的两部分.
,使PQ将菱形ABCD的面积恰好分成1:5的两部分.
【解析】(1)根据函数图象中E点所代表的实际意义求解.E点表示点P运动到与点B重合时的情形,运动时间为3s,可得AB=6cm;再由S△APQ= ![]() ,可求得AQ的长度,进而得到点Q的运动速度;(2)函数图象中线段FG,表示点Q运动至终点D之后停止运动,而点P在线段CD上继续运动的情形.如答图2所示,求出S的表达式,并确定t的取值范围;(3)当点P在AB上运动时,PQ将菱形ABCD分成△APQ和五边形PBCDQ两部分,如答图3所示,求出t的值;
,可求得AQ的长度,进而得到点Q的运动速度;(2)函数图象中线段FG,表示点Q运动至终点D之后停止运动,而点P在线段CD上继续运动的情形.如答图2所示,求出S的表达式,并确定t的取值范围;(3)当点P在AB上运动时,PQ将菱形ABCD分成△APQ和五边形PBCDQ两部分,如答图3所示,求出t的值;
当点P在BC上运动时,PQ将菱形分为梯形ABPQ和梯形PCDQ两部分,如答图4所示,求出t的值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用题:
某管道由甲、乙两工程队单独施工分别需要30天、20天.
(1)如果两队从管道两端同时施工,需要多少天完工?
(2)又知甲队单独施工每天需付200元施工费,乙队单独施工每天需付280元施工费,那么是由甲队单独施工,还是由乙队单独施工,还是由两队同时施工?请你按照少花钱多办事的原则,设计一个方案,并通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】考试前,同学们总会采用各种方式缓解考试压力,以最佳状态迎接考试.某校对该校九年级的部分同学做了一次内容为“最适合自己的考前减压方式”的调查活动,学校将减压方式分为五类,同学们可根据自己的情况必选且只选其中一类.学校收集整理数据后,绘制了图1和图2两幅不完整的统计图,请根据统计图中信息解答下列问题:
(1)这次抽样调查中,一共抽查了多少名学生?
(2)请补全条形统计图;
(3)请计算扇形统计图中“享受美食”所对应扇形的圆心角的度数;
(4)根据调查结果,估计该校九年级500名学生中采用“听音乐”来减压方式的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骰子是一种特别的数字立方体(见右图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )
![]()
A.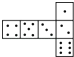 B.
B.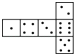 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店王阿姨到水果批发市场打算购进一种水果销售,经过还价,实际价格每千克比原来少2元,发现原来买这种水果80千克的钱,现在可买88千克.
(1)现在实际购进这种水果每千克多少元?
(2)王阿姨准备购进这种水果销售,若这种水果的销售量y(千克)与销售单价x(元/千克)满足如图所示的一次函数关系. ①求y与x之间的函数关系式;
②请你帮王阿姨拿个主意,将这种水果的销售单价定为多少时,能获得最大利润?最大利润是多少?(利润=销售收入﹣进货金额)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com