
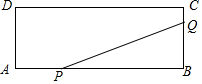
 如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).
如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).分析 (1)分别表示出PB、BQ的长,然后根据三角形的面积公式列式整理即可得解;
(2)把函数关系式整理成顶点式解析式,然后根据二次函数的最值问题解答.
解答 解:(1)∵S△PBQ=$\frac{1}{2}$PB•BQ,PB=AB-AP=18-2x,BQ=x,
∴y=$\frac{1}{2}$ (18-2x)x,
即y=-x2+9x(0<x≤4);
(2)由(1)知,y=-x2+9x,
∴y=-$(x-\frac{9}{2})^{2}+\frac{81}{4}$,
∵当0<x≤$\frac{9}{2}$时,y随x的增大而增大,
而0<x≤4,
∴当x=4时,y最大值=20,
即△PBQ的最大面积是20 cm2.
点评 本题考查了矩形的性质,二次函数的最值问题,根据题意表示出PB、BQ的长度是解题的关键.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
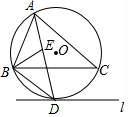 如图,⊙O是△ABC的外接圆,直线l与⊙O相切于点D,且l∥BC.
如图,⊙O是△ABC的外接圆,直线l与⊙O相切于点D,且l∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知P是两直角边分别为3cm、4cm的Rt△ABC斜边AB上的任意一点,以CP为直径作圆,则该圆的面积y(cm2)与CP的长x(cm)之间的函数关系式是y=$\frac{1}{4}$πx2,自变量x的取值范围是2.4≤x≤4,y的最小值是1.44π,y的最大值是4π.
如图,已知P是两直角边分别为3cm、4cm的Rt△ABC斜边AB上的任意一点,以CP为直径作圆,则该圆的面积y(cm2)与CP的长x(cm)之间的函数关系式是y=$\frac{1}{4}$πx2,自变量x的取值范围是2.4≤x≤4,y的最小值是1.44π,y的最大值是4π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 三角形的个数 | 1 | 2 | 3 | 4 | … |
| 火柴棒的根数 | 3 | 5 | 7 | 9 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com