
分析 把△ACM绕C点逆时针旋转90°,得△CBD,这样∠ACM+∠BCN=45°就集中成一个与∠MCN相等的角,在一条直线上的m、x、n集中为△DNB,只需判定△DNB的形状即可.
解答 解:结论:以x、m、n为边长的三角形是直角三角形.
理由:如图所示,把△ACM绕C点逆时针旋转90°,得△CBD,连接DN,
∵△ACM≌△BCD,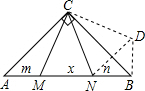
∴∠ACM=∠BCD,CM=CD,∠MCN=∠NCD=45°,
在△MNC与△DNC中,
∵$\left\{\begin{array}{l}{CM=CD}\\{∠MCN=∠NCD}\\{CN=CN}\end{array}\right.$,
∴△MNC≌△DNC(SAS),
∴MN=ND,AM=BD=m,
又∵∠DBN=45°+45°=90°,
∴以x、m、n为边长的三角形的形状为直角三角形.
点评 本题考查等腰直角三角形的性质,难度较大,注意掌握下列情形常实施旋转变换:(1)图形中出现等边三角形或正方形,把旋转角分别定为60°、90°;(2)图形中有线段的中点,将图形绕中点旋转180°,构造中心对称全等三角形;(3)图形中出现有公共端点的线段,将含有相等线段的图形绕公共端点,旋转两相等线段的夹角后与另一相等线段重合.


科目:初中数学 来源: 题型:解答题
 如图,已知AD⊥EF,CE⊥EF,∠2+∠3=180°.
如图,已知AD⊥EF,CE⊥EF,∠2+∠3=180°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
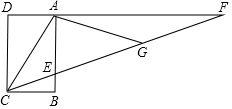 “三等分一个任意角”是数学史上一个著名问题,今天人们已经知道,仅用圆规直尺是不可能做出的.在探索中,有人曾利用过如图所示的图形,其中,ABCD是长方形(AD∥CB),F是DA延长线上一点,G 是CF上一点,并且∠ACG=∠AGC,∠GAF=∠F,你能证明∠ECB=$\frac{1}{3}$∠ACB吗?
“三等分一个任意角”是数学史上一个著名问题,今天人们已经知道,仅用圆规直尺是不可能做出的.在探索中,有人曾利用过如图所示的图形,其中,ABCD是长方形(AD∥CB),F是DA延长线上一点,G 是CF上一点,并且∠ACG=∠AGC,∠GAF=∠F,你能证明∠ECB=$\frac{1}{3}$∠ACB吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
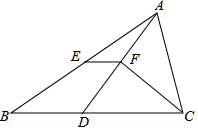 如图.在△ABC中,BC>AC,点D在BC上,且CD=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连接EF.
如图.在△ABC中,BC>AC,点D在BC上,且CD=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连接EF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 秒 | B. | 6秒 | C. | 8 秒 | D. | 10秒 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
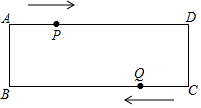 如图,在矩形ABCD中,AB=4cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在这段时间内,线段PQ有( )次平行于AB?
如图,在矩形ABCD中,AB=4cm,AD=12cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在这段时间内,线段PQ有( )次平行于AB?| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com