
【题目】A、B两地相距50km,甲于某日骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地,在这个变化过程中,甲和乙所行驶的路程用变量s(km)表示,甲所用的时间用变量t(时)表示,图中折线OPQ和线段MN分别表示甲和乙所行驶的路程s与时间t的变化关系,请根据图象回答:

(1)直接写出:甲出发后______小时,乙才开始出发;
(2)请分别求出甲出发1小时后的速度和乙的行驶速度?
(3)求乙行驶几小时后追上甲,此时两人距B地还有多少千米?
【答案】(1)1;(2)甲:25km/h,乙:10km/h;(3)乙行驶![]() 小时后追上甲,此时两人距
小时后追上甲,此时两人距![]() 地还有
地还有![]() 千米
千米
【解析】
(1)观察函数图象得到甲出发后1小时,乙才开始出发;
(2)根据路程除以时间等于速度,列式求解即可得到答案;
(3)设乙行驶![]() 小时后追上甲,根据题意得
小时后追上甲,根据题意得![]() ,求解即可得到答案;
,求解即可得到答案;
解:(1)观察函数图象得到甲出发后1小时,乙才开始出发,
故填:1;
(2)由图像信息可知:乙的速度为:![]() 千米/时,
千米/时,
甲出发1小时后的速度为:![]() 千米/时.
千米/时.
(3)设乙行驶![]() 小时后追上甲,结合图片信息和(2)的结果得到:
小时后追上甲,结合图片信息和(2)的结果得到:
![]() ,
,
解得![]() ,
,
即乙行驶![]() 小时后追上甲,此时两人距
小时后追上甲,此时两人距![]() 地还有
地还有![]() (千米);
(千米);
答:乙行驶![]() 小时后追上甲,此时两人距
小时后追上甲,此时两人距![]() 地还有
地还有![]() 千米;
千米;


科目:初中数学 来源: 题型:
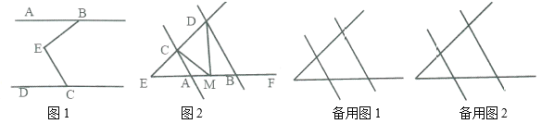
【题目】操作探究:
(1)实践:如图1, ![]() 中,
中,![]() 为
为![]() 边上的中线,
边上的中线,![]() 的面积记为
的面积记为![]() ,
,![]() 的面积记为
的面积记为![]() .则
.则![]() .
.

(2)探究:在图2中,![]() 、
、![]() 分别为四边形
分别为四边形![]() 的边
的边![]() 、
、![]() 的中点,四边形
的中点,四边形![]() 的面积记为
的面积记为![]() ,阴影部分面积记为
,阴影部分面积记为![]() ,则
,则![]() 和
和![]() 之间满足的关系式为______:
之间满足的关系式为______:
(3)解决问题:
在图3中,![]() 、
、![]() 、
、![]() 、
、![]() 分别为任意四边形
分别为任意四边形![]() 的边
的边![]() 、
、![]() 、
、![]() 、
、![]() 的中点,并且图中阴影部分的面积为
的中点,并且图中阴影部分的面积为![]() 平方厘米,求图中四个小三角形的面积和,并说明理由.
平方厘米,求图中四个小三角形的面积和,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种事物经历了加热,冷却两个联系过程,折线图DEF表示食物的温度y(℃)与时间x(s)之间的函数关系(0≤x≤160),已知线段EF表示的函数关系中,时间每增加1s,食物温度下降0.3℃,根据图象解答下列问题;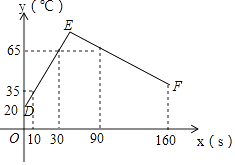
(1)当时间为20s、100s时,该食物的温度分别为℃,℃;
(2)求线段DE所表示的y与x之间的函数表达式;
(3)时间是多少时,该食物的温度最高?最高是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)、求证:四边形AODE是矩形;(2)、若AB=6,∠BCD=120°,求四边形AODE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC,△CDE均为等边三角形(每个内角都是60°),连接BD,AE交于点O,BC与AE交于点P.试说明:∠POB=60°.经过观察分析,解题的关键是先利用( )说明△EAC≌△DBC.

A.SSSB.ASAC.SASD.AAS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,点
,点![]() 为平面内一点.
为平面内一点.
(1)如图1,![]() 和
和![]() 互余,小明说过
互余,小明说过![]() 作
作![]() ,很容易说明
,很容易说明![]() 。请帮小明写出具体过程;
。请帮小明写出具体过程;
(2)如图2,![]() ,当点
,当点![]() 在线段
在线段![]() 上移动时(点
上移动时(点![]() 与
与![]() ,
,![]() 两点不重合),指出
两点不重合),指出![]() 与
与![]() ,
,![]() 的数量关系?请说明理由;
的数量关系?请说明理由;
(3)在(2)的条件下,若点![]() 在
在![]() ,
,![]() 两点外侧运动(点
两点外侧运动(点![]() 与
与![]() ,
,![]() ,
,![]() 三点不重合)请直接写出
三点不重合)请直接写出![]() 与
与![]() ,
,![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
跳绳数/个 | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
人 数 | 1 | 2 | 8 | 11 | 5 |
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).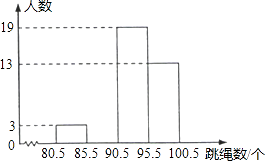
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次跳绳成绩的众数是个,中位数是个;
(3)若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:Rt△ABC中,∠C=90°,AC=BC=2,将一块三角尺的直角顶点与斜边AB的中点M重合,当三角尺绕着点M旋转时,两直角边始终保持分别与边BC、AC交于D,E两点(D、E不与B、A重合).
(1)求证:MD=ME;
(2)求四边形MDCE的面积;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(1,0)、B(3,0).抛物线y=x2﹣2mx+m2﹣4的顶点为P,与y轴的交点为Q.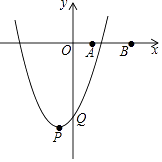
(1)填空:点P的坐标为;点Q的坐标为(均用含m的代数式表示)
(2)当抛物线经过点A时,求点Q的坐标.
(3)连接QA、QB,设△QAB的面积为S,当抛物线与线段AB有公共点时,求S与m之间的函数关系式.
(4)点P、Q不重合时,以PQ为边作正方形PQMN(P、Q、M、N分别按顺时针方向排列).当正方形PQMN的四个顶点中,位于x轴两侧或y轴两侧的顶点个数相同时,直接写出此时m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com