
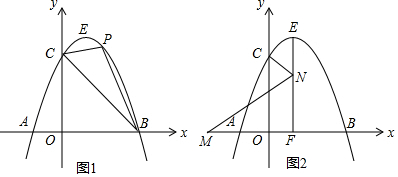
���� ��1��������֪�������y=-x2+2x+3����x=0ʱ���õ�y=3�����ǵõ�C��0��3����
��2��������-x2+2x+3=0����õ�B�����꣬Ȼ����ֱ��BC�Ľ���ʽΪy=kx+b�䣬�ɴ���ϵ�����������ֱ��BC�Ľ���ʽ������Q��a��3-a�������ɵ�P��a��-a2+2a+3�����������PQ�ij�����S��PBC=S��PQC+S��PQB�����ɵ�S��PBC=-$\frac{3}{2}$��a-$\frac{3}{2}$��2+$\frac{27}{8}$�����ö��κ��������ʣ�������õ���BDC��������ʱ�����P�����ꣻ��3�����ȹ�C��CH��EF��H�㣬��CH=EH=1��Ȼ��ֱ�ӵ�M��EF�����M��EF�Ҳ�ʱȥ������⼴����ô𰸣�
��� �⣺��1����������y=ax2+bx+c�Ķ�������ΪE��1��4����
����y=a��x-1��2+4��
��B��3��0�����룬��0=a��3-1��2+4��
��ã�a=-1��
��y=-��x-1��2+4��
��y=-x2+2x+3��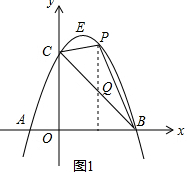
��x=0ʱ��y=3��
��C��0��3����
��2������ͼ1����P��PQ��y��BC�ڵ�Q��
��ֱ��BC�Ľ���ʽΪ��y=kx+b��
��$\left\{\begin{array}{l}3k+b=0\\ b=3\end{array}\right.$
���$\left\{\begin{array}{l}k=-1\\ b=3\end{array}\right.$
��ֱ��BC�Ľ���ʽΪy=-x+3��
��P��t��-t2+2t+3����Q��t��-t+3����
��PQ=��-t2+2t+3��-��-t+3��
=-t2+3t��
���PBC�����s=$\frac{1}{2}��3$��-t2+3t��
=$-\frac{3}{2}{��\;t-\frac{3}{2}\;��^2}+\frac{27}{8}$��
�൱t=$\frac{3}{2}$ʱ����PBC��������Ϊ$\frac{27}{8}$��
�ڡߡ�PBC��90�㣬
�����PCB=90��ʱ��
��ֱ��PC�Ľ���ʽΪ��y=kx+b��
��CP��BC
��k=1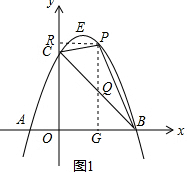
��ֱ��PC�Ľ���ʽΪy=x+3��
��$\left\{\begin{array}{l}y=-{x^2}+2x+3\\ y=x+3\end{array}\right.$��
��$\left\{\begin{array}{l}x=1\\ y=4\end{array}\right.$��$\left\{\begin{array}{l}x=0\\ y=3\end{array}\right.$���ᣩ��
��t=1��
����BPC=90��ʱ��
��ͼ1����P��PG��x����G����PR��y����R��
��֪��PRC�ס�PGB��
��$\frac{RC}{PR}=\frac{BG}{PG}$��
��$\frac{{-{t^2}+2t}}{t}=\frac{3-t}{{-{t^2}+2t+3}}$��
��t��0��t��3��
��$\frac{-t+2}{1}=\frac{1}{t+1}$
��t2-t-1=0
���$t=\frac{{1��\sqrt{5}}}{2}$��
��$t=\frac{{1+\sqrt{5}}}{2}$��
��3���ɣ�1��֪��y=-x2+2x+3=-��x-1��2+4��
��OF=1��EF=4��OC=3��
��C��CH��EF��H�㣬��CH=EH=1��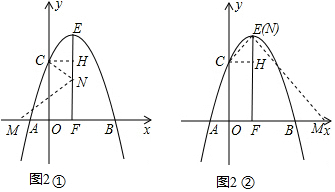
��ͼ2�٣���M��EF���ʱ��
�ߡ�MNC=90�㣬
���MNF�ס�NCH��
��$\frac{MF}{NH}$=$\frac{FN}{HC}$��
��FN=n����NH=3-n��
��$\frac{1-m}{3-n}$=$\frac{n}{1}$��
��n2-3n-m+1=0��
����n�ķ����н⣬��=��-3��2-4��-m+1����0��
��m��-$\frac{5}{4}$��m��1��
��M��F�غ�ʱ��m=1��
��ͼ2�ڣ���M��EF�Ҳ�ʱ��Rt��CHE�У�CH=EH=1����CEH=45�㣬����CEF=45�㣬
��EM��CE��x���ڵ�M�����FEM=45�㣬
��FM=EF=4��
��OM=5��
��NΪ��Eʱ��OM=5��
��m��5��
���ϣ�m�ı仯��ΧΪ��-$\frac{5}{4}$��m��5��
���� ���⿼���˴���ϵ���������Ľ���ʽ�����������ε��ж������ʡ����κ�������ֵ���⡢�б�ʽ��Ӧ���Լ�����ֱ�������ε����ʵ�֪ʶ�������ۺ��Ժ�ǿ���ѶȽϴ�ע���������ν��˼�롢��������˼���뷽��˼���Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
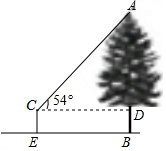 ��ͼ������С��Ҫ��������һ�����ĸ߶�AB������һ��С���Ավ�ھ�����10�ĵ�E�����������A������Ϊ54�㣮��֪����ǵļܸ�CE=1.5�ף���������ĸ߶�Ϊ15.3�ף����������һλС�����ο����ݣ�sin54��=0.8090��cos54��=0.5878��tan54��=1.3764��
��ͼ������С��Ҫ��������һ�����ĸ߶�AB������һ��С���Ավ�ھ�����10�ĵ�E�����������A������Ϊ54�㣮��֪����ǵļܸ�CE=1.5�ף���������ĸ߶�Ϊ15.3�ף����������һλС�����ο����ݣ�sin54��=0.8090��cos54��=0.5878��tan54��=1.3764���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
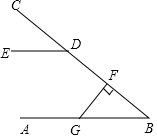 ��ͼ��AB��DE��FG��BC��F����CDE=40�㣬���FGB=��������
��ͼ��AB��DE��FG��BC��F����CDE=40�㣬���FGB=��������| A�� | 40�� | B�� | 50�� | C�� | 60�� | D�� | 70�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
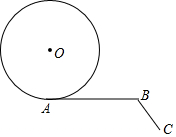 ��ͼ����֪��ABC=120�㣬AB=��r��BC=$\frac{��r}{2}$���뾶Ϊr�ġ�O�ӵ�A��������A��B��C�����������Cʱֹͣ����Բ��O�˶���·����$\frac{11}{6}$��r��
��ͼ����֪��ABC=120�㣬AB=��r��BC=$\frac{��r}{2}$���뾶Ϊr�ġ�O�ӵ�A��������A��B��C�����������Cʱֹͣ����Բ��O�˶���·����$\frac{11}{6}$��r���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
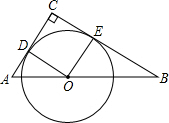 ��ͼ���ڡ�ABC�У���C=90�㣬��O��б��AB��һ�㣬��OΪԲ�ĵġ�O�ֱ����AC��BC�����ڵ�D��E������OD��OE��
��ͼ���ڡ�ABC�У���C=90�㣬��O��б��AB��һ�㣬��OΪԲ�ĵġ�O�ֱ����AC��BC�����ڵ�D��E������OD��OE���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com