
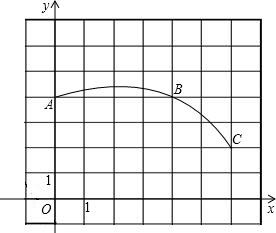
如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
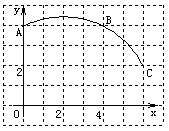
(1) 请在图中确定该圆弧所在圆心D点的位置,D点坐标为________;
(2) 连接AD、CD,求⊙D的半径(结果保留根号)及扇形ADC的圆心角度数;
(3) 若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径 (结果保留根号).
(1) D(2,0);(2)半径为 ,圆心角为90度;(3)
,圆心角为90度;(3) 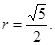
【解析】
试题分析:(1)根据垂径定理的推论:弦的垂直平分线必过圆心,即可作出弦AB,BC的垂直平分线,交点即为圆心;
(2)根据勾股定理进行计算,连接DA,DC,根据SAS得到两个三角形全等△AOD≌△DCE,则∠ADC=90°;
(3)根据圆锥的底面周长等于弧长,进行计算.
(1)如图:D(2,0);
(2)如图: ,
,
作CE⊥x轴,垂足为E,

∵△AOD≌△DEC
∴∠OAD=∠CDE
又∵∠OAD+∠ADO=90°
∴∠CDE+∠ADO=90°
∴扇形DAC的圆心角为90度;
(3)方法一:
∵弧AC的长度即为圆锥底面圆的周长.

设圆锥底面圆半径为r,则 ,解得
,解得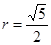 ;
;
方法二:圆锥的侧面积 ,其中母线l即为⊙D的半径
,其中母线l即为⊙D的半径 ,r为圆锥的底面半径.
,r为圆锥的底面半径.
又扇形DAC的面积:
∴
解得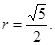
考点:本题考查的是圆锥的计算,坐标与图形性质,确定圆的条件
点评:解答本题的关键是能够根据垂径定理作出圆的圆心,根据全等三角形的性质确定角之间的关系,掌握圆锥的底面半径的计算方法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
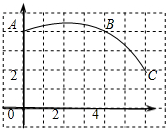 如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2009-2010学年江苏省南京市六中九年级(上)期末数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第27章《圆(一)》常考题集(19):27.4 弧长和扇形面积(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第24章《圆》常考题集(31):24.4 弧长和扇形面积(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com