
分析 (1)移项后利用直接开平方法解答;
(2)化为一般形式后用十字相乘法解答;
(3)因式分解后用直接开平方法解答;
(4)用直接开平方法解答;
(5)将(2x+3)看作整体,用十字相乘法解答.
解答 解:(1)(y-3)2-5=0,
移项得,(y-3)2=5,
开方得,y-3=±$\sqrt{5}$,
y1=3+$\sqrt{5}$,y2=3-$\sqrt{5}$.
(2)(x-1)(x+2)=54,
方程可化为x2+x-56=0,
解得(x-7)(x+8)=0,
x1=7,x2=-8.
(3)x2-6x+9=(5-2x)2
方程可化为(x-3)2=(5-2x)2,
解得x-3=±(5-2x),
解得x1=$\frac{8}{3}$,x2=2.
(4)(x+$\sqrt{2}$)2=8
解得,x+$\sqrt{2}$=±2$\sqrt{2}$,
解得,x1=$\sqrt{2}$,x2=-3$\sqrt{2}$.
(5)(2x+3)2-5(2x+3)+4=0,
因式分解得,(2x+3-1)(2x+3-4)=0,
解得x1=-1,x2=$\frac{1}{2}$.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1,$\frac{2}{3}$) | B. | (-2,$\frac{1}{3}$) | C. | (1,-$\frac{2}{3}$) | D. | (-$\frac{1}{3}$,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在东西方向的海岸线一观测点A处,某时刻测得一艘匀速直线航行的渔船位于A的东偏北30°方向,且与点A相距20$\sqrt{3}$千米的B处,经过40分钟,该渔船在与A相距20千米的C处靠岸,求该渔船航行的速度.
如图,在东西方向的海岸线一观测点A处,某时刻测得一艘匀速直线航行的渔船位于A的东偏北30°方向,且与点A相距20$\sqrt{3}$千米的B处,经过40分钟,该渔船在与A相距20千米的C处靠岸,求该渔船航行的速度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,EF过对角线的交点O,且与边AB、CD分别相交于点E、F、AB=4,AD=3,OF=1.3,求四边形BCFE的周长.
如图,在?ABCD中,EF过对角线的交点O,且与边AB、CD分别相交于点E、F、AB=4,AD=3,OF=1.3,求四边形BCFE的周长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
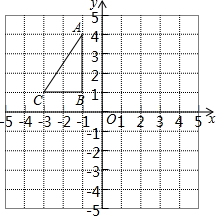 如图,在平面直角坐标系中,Rt△ABC的三个顶点均在边长为1的正方形网格格点上.
如图,在平面直角坐标系中,Rt△ABC的三个顶点均在边长为1的正方形网格格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com