
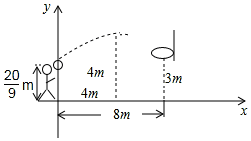
 小明跳起投篮,球出手时离地面$\frac{20}{9}$m,球出手后在空中沿抛物线路径运动,并在距出手点水平距离4m处达到最高4m.已知篮筐中心距地面3m,与球出手时的水平距离为8m,建立如图所示的平面直角坐标系.
小明跳起投篮,球出手时离地面$\frac{20}{9}$m,球出手后在空中沿抛物线路径运动,并在距出手点水平距离4m处达到最高4m.已知篮筐中心距地面3m,与球出手时的水平距离为8m,建立如图所示的平面直角坐标系.分析 (1)根据顶点坐标(4,4),设抛物线的解析式为:y=a(x-4)2+4,由球出手时离地面$\frac{20}{9}$m,可知抛物线与y轴交点为(0,$\frac{20}{9}$),代入可求出a的值,写出解析式;
(2)先计算当x=8时,y的值是否等于3,把x=8代入得:y=$\frac{20}{9}$,所以要想球经过(8,3),则抛物线得向上平移3-$\frac{20}{9}$=$\frac{7}{9}$个单位,即球出手时距离地面3米可使球直接命中篮筐中心.
解答 解:(1)设抛物线为y=a(x-4)2+4,
将(0,$\frac{20}{9}$)代入,得a(0-4)2+4=$\frac{20}{9}$,
解得a=-$\frac{1}{9}$,
∴所求的解析式为y=-$\frac{1}{9}$(x-4)2+4;
(2)令x=8,得y=-$\frac{1}{9}$(8-4)2+4=$\frac{20}{9}$≠3,
∴抛物线不过点(8,3),
故不能正中篮筐中心;
∵抛物线过点(8,$\frac{20}{9}$),
∴要使抛物线过点(8,3),可将其向上平移$\frac{7}{9}$个单位长度,故小明需向上多跳$\frac{7}{9}$m再投篮(即球出手时距离地面3米)方可使球正中篮筐中心.
点评 本题是二次函数的应用,属于常考题型,此类题的解题思路为:①先根据已知确定其顶点和与y轴交点或x轴交点,求解析式;②根据图形中的某点坐标得出相应的结论.


 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:长方形ABCD中,AB=3,AD=9,将此长方形折叠,使点B与点D重合,折痕EF交AD于E,交BC于F.请用直尺和圆规画出折痕EF,并求出△ABE的面积.(长方形的对边平行且相等,四个角都为直角)
已知:长方形ABCD中,AB=3,AD=9,将此长方形折叠,使点B与点D重合,折痕EF交AD于E,交BC于F.请用直尺和圆规画出折痕EF,并求出△ABE的面积.(长方形的对边平行且相等,四个角都为直角)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com