
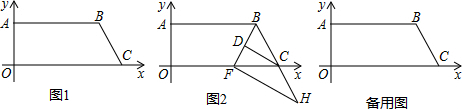
分析 (1)根据点C向左平移4单位长度再向上平移7个单位长度得到对应点B的坐标;
(2)结论:DC∥FH.只要证明CD⊥BF即可;
(3)先根据动点P、Q的速度表示出路程分别为:2t、t,再根据面积公式表示出S1和S2,代入S1<2S2列不等式求t的取值范围,并与0<t<7相结合得出t的取值.
解答 解:(1)由题意点B的坐标(14,7);
故答案为(14,7).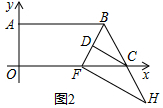
(2)结论:PC∥FH.
理由如下:∵BF平分∠ABC
∴∠FBC=$\frac{1}{2}$∠ABC
∵CD平分∠BCO,
∴∠BCD=$\frac{1}{2}$∠BCO
依题意得A(0,7),B(14,7),
∴AB⊥y轴,
∴AB∥OC
∴∠ABC+∠BCO=180°
∴∠FBC+∠BCD=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠BCO=$\frac{1}{2}$(∠ABC+∠BCO)=$\frac{1}{2}$×180°=90°,
∴∠BPC=180°-(∠FBC+∠BCP)=90°
∴CP⊥BF,
∵FH⊥BF
∴PC∥FH.
(3)存在
如图3中,由(1)得B(14,7)
由题意得:PC=2t,OQ=t,则OP=18-2t,A(0,7),C(18,0),
S1=$\frac{1}{2}$(AB+OP)×OA=$\frac{1}{2}$(14+18-2t)×7=-7t+112(6分)
S2=$\frac{1}{2}$t×14=7t(7分)
∵要满足S1<2S2
∴-7t+112<2×7t(8分)
t>$\frac{16}{3}$,
又∵0<t<7
∴当$\frac{16}{3}$<t<7时,S1<2S2.
点评 本题是几何变换的综合题,平行线的性质、点的坐标与平移的关系,还考查了动点在运动过程中所形成的图形面积问题,此类题的解题思路为:先表示动点的路程,再根据图形形状直接或间接利用和、差表示图形面积.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:填空题
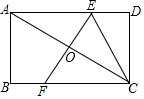 如图,在矩形ABCD中,AB=3,∠BCA=30°,对角线AC的垂直平分线分别交AD,BC于点E、F,连接CE,则CE的长为2$\sqrt{3}$.
如图,在矩形ABCD中,AB=3,∠BCA=30°,对角线AC的垂直平分线分别交AD,BC于点E、F,连接CE,则CE的长为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
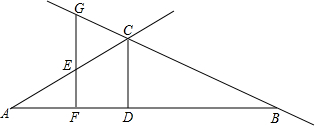 如图,已知CD⊥AB于D,E是射线AC上一动点,EF⊥AB于F,EF交直线BC于G,若∠AEF=∠CGE.
如图,已知CD⊥AB于D,E是射线AC上一动点,EF⊥AB于F,EF交直线BC于G,若∠AEF=∠CGE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com