
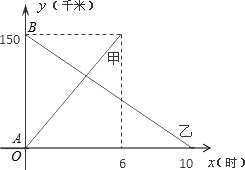
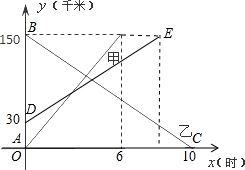
 A、B两码头相距150千米,甲客船顺流由A航行到B,乙客船逆流由B到A,若甲、乙两客船在静水中的速度相同,同时出发,它们距A的距离y(千米)与航行时间x(时)的关系如图所示.
A、B两码头相距150千米,甲客船顺流由A航行到B,乙客船逆流由B到A,若甲、乙两客船在静水中的速度相同,同时出发,它们距A的距离y(千米)与航行时间x(时)的关系如图所示.| 150 |
| 6 |
| 150 |
| 10 |
|
|
|
|
|
|
|
|


科目:初中数学 来源:课外练习 七年级数学 下 题型:044
列方程组解应用题:
长江沿岸有两个码头相距240 km,一艘货轮在其间航行,顺流需要12小时,逆流需要15小时,求这艘轮船在静水中的速度和水流速度.(顺水速度=静水速度+水流速度,逆水速度=静水速度-水流速度)
查看答案和解析>>
科目:初中数学 来源:1课1测七年级数学(上) 题型:044
某船从A码头顺流航行到B码头,然后逆流返航到C码头,共行9小时,已知船在静水中的速度为7.5千米/时,水流速度为2.5千米/时,若A与C两码头相距15千米,求A与B间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com