
【题目】如图,在平面直角坐标系中,![]() 为原点,
为原点,![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,以
,以![]() 为直径的圆
为直径的圆![]() 与
与![]() 轴的负半轴交于点
轴的负半轴交于点![]() .
.
(1)求图象经过![]() ,
,![]() ,
,![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(2)设![]() 点为所求抛物线的顶点,试判断直线
点为所求抛物线的顶点,试判断直线![]() 与
与![]() 的关系,并说明理由.
的关系,并说明理由.

【答案】(1)![]() (2)直线
(2)直线![]() 与
与![]() 相切,理由见解析
相切,理由见解析
【解析】
(1)已知A、B两点的坐标,要求抛物线的解析式,即要求点C的坐标,由相似三角形的判定与性质求出OC的长度,即可求出点C的坐标;(2)根据抛物线解析式求出点M的坐标,分别求出MP、CP、CM的长度,利用勾股定理逆定理判定△CPM为直角三角形,从而得出PC⊥MC,所以直线MC与⊙P相切.
解:(1)连接AC、BC;
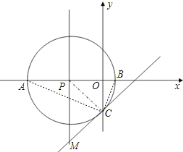
∵AB是⊙P的直径,
∴∠ACB=90°,即∠ACO+∠BCO=90°,
∵∠BCO+∠CBO=90°,
∴∠CBO=∠ACO,
∵∠AOC=∠BOC=90°,
∴△AOC∽△COB,
∴![]() =
=![]() ,
,
∴OC2=OA·OB=16,
∴OC=4,
故C(0,﹣4),
设抛物线的解析式为:y=a(x+8)(x﹣2),
代入C点坐标得:a(0+8)(0﹣2)=﹣4,a=![]() ,
,
故抛物线的解析式为:y=![]() (x+8)(x﹣2)=
(x+8)(x﹣2)=![]() +
+![]() x﹣4;
x﹣4;
(2)由(1)知:y=![]() +
+![]() x﹣4=
x﹣4=![]() ﹣
﹣![]() ;
;
则M(﹣3,﹣![]() ),
),
又∵C(0,﹣4),P(﹣3,0),
∴MP=![]() ,PC=5,MC=
,PC=5,MC=![]() ,
,
∴MP2=MC2+PC2,即△MPC是直角三角形,且∠PCM=90°,
故直线MC与⊙P相切.


科目:初中数学 来源: 题型:
【题目】连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )

A. ![]() 是等边三角形
是等边三角形
B. 连接![]() ,则
,则![]() 分别平分
分别平分![]() 和
和![]()
C. 整个图形是轴对称图形,但不是中心对称图形
D. 四边形![]() 与四边形
与四边形![]() 的面积相等
的面积相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数![]() 的图象,
的图象,![]() 、
、![]() 、
、![]() 为抛物线与坐标轴的交点,且
为抛物线与坐标轴的交点,且![]() ,则下列关系中正确的是( )
,则下列关系中正确的是( )

A. ac<0 B. b<2a C. a+b=-1 D. a-b=-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,圆柱底面半径为![]() ,高为
,高为![]() ,点
,点![]() 分别是圆柱两底面圆周上的点,且
分别是圆柱两底面圆周上的点,且![]() 、
、![]() 在同一母线上,用一棉线从
在同一母线上,用一棉线从![]() 顺着圆柱侧面绕3圈到
顺着圆柱侧面绕3圈到![]() ,求棉线最短为_________
,求棉线最短为_________![]() 。
。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市计划建造一座如图设计的塔形建筑物作为市标,最底层的圆柱形的底面半径为![]() ,高为
,高为![]() 米,再上去的圆柱形底面半径以
米,再上去的圆柱形底面半径以![]() 的比例缩小,而楼层的高度也以同样的比例缩小,那么要使得建筑物的表面积不超过
的比例缩小,而楼层的高度也以同样的比例缩小,那么要使得建筑物的表面积不超过![]() 平方米(表面积不包括最底层的底面积),楼层最高为________层.
平方米(表面积不包括最底层的底面积),楼层最高为________层.![]() 取
取![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC放置在每个小正方形边长为1的网格中,点A,B,C均在格点上,建立适当的平面直角坐标系xOy,△ABC与△A′B′C′关于y轴对称.

(1)画出该平面直角坐标系与△A′B′C′.
(2)在y轴上找点P,使PC+PB′的值最小,求点P的坐标与PC+PB'的最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学们设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试,根据测试成绩分布情况,他们将全部测试成绩分成A、B、C、D四组,绘制了如下统计图表:
“垃圾分类知识及投放情况”问卷测试成绩统计图表
组别 | 分数/分 | 频数 | 各组总分/分 |
A | 60<x≤70 | 38 | 2 581 |
B | 70<x≤80 | 72 | 5 543 |
C | 80<x≤90 | 60 | 5 100 |
D | 90<x≤100 | m | 2 796 |

依据以上统计信息,解答下列问题:
(1)求得m=________,n=__________;
(2)这次测试成绩的中位数落在______组;
(3)求本次全部测试成绩的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家去李宁体育馆游泳,同时,妈妈从李宁体育馆以50米/分的速度回家,小明到体育馆后发现要下雨,立即返回,追上妈妈后,小明以250米/分的速度回家取伞,立即又以250米/分的速度折回接妈妈,并一同回家.如图是两人离家的距离y(米)与小明出发的时间x(分)之间的函数图像.(注:小明和妈妈始终在同一条笔直的公路上行走,图像上A、C、D、F四点在一条直线上)

(1)求线段oB及线段AF的函数表达式;
(2)求C点的坐标及线段BC的函数表达式;
(3)当x为 时,小明与妈妈相距1500米;
(4)求点D坐标,并说明点D的实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践﹣猜想、证明与拓广
问题情境:
数学课上同学们探究正方形边上的动点引发的有关问题,如图1,正方形ABCD中,点E是BC边上的一点,点D关于直线AE的对称点为点F,直线DF交AB于点H,直线FB与直线AE交于点G,连接DG,CG.
猜想证明
(1)当图1中的点E与点B重合时得到图2,此时点G也与点B重合,点H与点A重合.同学们发现线段GF与GD有确定的数量关系和位置关系,其结论为: ;
(2)希望小组的同学发现,图1中的点E在边BC上运动时,(1)中结论始终成立,为证明这两个结论,同学们展开了讨论:
小敏:根据轴对称的性质,很容易得到“GF与GD的数量关系”…
小丽:连接AF,图中出现新的等腰三角形,如△AFB,…
小凯:不妨设图中不断变化的角∠BAF的度数为n,并设法用n表示图中的一些角,可证明结论.
请你参考同学们的思路,完成证明;
(3)创新小组的同学在图1中,发现线段CG∥DF,请你说明理由;
联系拓广:
(4)如图3若将题中的“正方形ABCD”变为“菱形ABCD“,∠ABC=α,其余条件不变,请探究∠DFG的度数,并直接写出结果(用含α的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com