
| A. | 1 | B. | 1或$\frac{\sqrt{3}-1}{2}$ | C. | 1或$\frac{\sqrt{3}+1}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$或$\frac{\sqrt{3}+1}{2}$ |
分析 延长AC,做PD⊥BC交点为D,PE⊥AC,交点为E,可得四边形CDPE是正方形,则CD=DP=PE=EC;等腰Rt△ABC中,∠C=90°,AC=1,所以,可求出AC=1,AB=$\sqrt{2}$,又AB=AP;所以,在直角△AEP中,可运用勾股定理求得DP的长即为点P到BC的距离.
解答 解:①如图1,延长AC,做PD⊥BC交点为D,PE⊥AC,交点为E,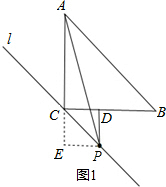
∵CP∥AB,
∴∠PCD=∠CBA=45°,
∴四边形CDPE是正方形,
则CD=DP=PE=EC,
∵在等腰直角△ABC中,AC=BC=1,AB=AP,
∴AB=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴AP=$\sqrt{2}$;
∴在直角△AEP中,(1+EC)2+EP2=AP2
∴(1+DP)2+DP2=($\sqrt{2}$)2,
解得,DP=$\frac{\sqrt{3}-1}{2}$;
②如图2,延长BC,作PD⊥BC,交点为D,延长CA,作PE⊥CA于点E,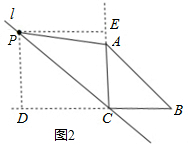
同理可证,四边形CDPE是正方形,
∴CD=DP=PE=EC,
同理可得,在直角△AEP中,(EC-1)2+EP2=AP2,
∴(PD-1)2+PD2=($\sqrt{2}$)2,
解得,PD=$\frac{\sqrt{3}+1}{2}$;
故选D.
点评 本题考查的是等腰直角三角形及勾股定理的运用,通过添加辅助线,可将问题转化到直角三角形中,利用勾股定理解答;考查了学生的空间想象能力.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
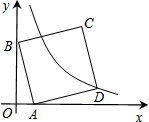 如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线上则a的值是( )
如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线上则a的值是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 甲 | 乙 | 丙 | 丁 | |
| 平均分 | 80 | 80 | 85 | 85 |
| 方 差 | 59 | 41 | 54 | 42 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com