
【题目】已知△ABC中,AB=AC,∠BAC=90°,D、E分别是AB、AC的中点,将△ADE绕点A按顺时针方向旋转一个角度α(0°<α<90°)得到△AD'E′,连接BD′、CE′,如图1.
(1)求证:BD′=CE';
(2)如图2,当α=60°时,设AB与D′E′交于点F,求![]() 的值.
的值.

【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)首先依据旋转的性质和中点的定义证明AD′=AE′,然后再利用SAS证明△BD′A≌△CE′A,最后,依据全等三角形的性质进行证明即可;
(2)连接DD′,先证明△ADD′为等边三角形,然后再证明△△ABD′为直角三角形,接下来,再证明△BFD′∽△AFE′,最后,依据相似三角形的性质求解即可.
(1)证明:∵AB=AC,D、E分别是AB、AC的中点,
∴AD=BD=AE=EC.
由旋转的性质可知:∠DAD′=∠EAE′=α,AD′=AD,AE′=AE.
∴AD′=AE′,
∴△BD′A≌△CE′A,
∴BD′=CE′.
(2)连接DD′.
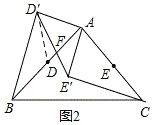
∵∠DAD′=60°,AD=AD′,
∴△ADD′是等边三角形.
∴∠ADD′=∠AD′D=60°,DD′=DA=DB.
∴∠DBD′=∠DD′B=30°,
∴∠BD′A=90°.
∵∠D′AE′=90°,
∴∠BAE′=30°,
∴∠BAE′=∠ABD′,
又∵∠BFD′=∠AFE′,
∴△BFD′∽△AFE′,
∴![]() .
.
∵在Rt△ABD′中,tan∠BAD′=![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】根据直尺和三角尺的实物摆放图,解决下列问题.



(1)如图1,是我们学过的用直尺和三角尺画平行线的方法的示意图,画图的原理是__________;
(2)如图2,图中互余的角有________________,若要使直尺的边缘DE与三角尺的AB边平行,则应满足_________(填角相等);
(3)如图3,若BC∥GH,试判断AC和FG的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年6月份,某果农收获荔枝30吨,香蕉13吨,现计划租用甲、乙两种货车共10辆将这批水果全部运往港口,已知一辆甲种货车可装荔枝和香蕉共5吨,且一辆甲种货车可装的荔枝重量(单位:吨)是其可装的香蕉重量的4倍,一辆乙种货车可装荔枝香蕉各2吨;
(1)一辆甲种货车可装载荔枝、香蕉各多少吨?
(2)该果农安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)若甲种货车每辆要付运输费2000元,乙种货车每辆要付运输费1300元,则该果农应选择哪种方案?使运费最少?最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,AB=4,点
,AB=4,点![]() 是边
是边![]() 上动点(点
上动点(点![]() 不与点
不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() ,交
,交![]() 边于点
边于点![]() .
.
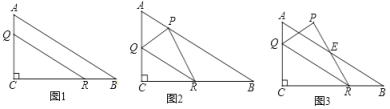
(1)求![]() 的大小;
的大小;
(2)若把![]() 沿着直线
沿着直线![]() 翻折得到
翻折得到![]() ,设
,设![]()
① 如图2,当点![]() 落在斜边
落在斜边![]() 上时,求
上时,求![]() 的值;
的值;
② 如图3,当点![]() 落在
落在![]() 外部时,
外部时,![]() 与
与![]() 相交于点
相交于点![]() ,如果
,如果![]() ,写出
,写出![]() 与
与![]() 的函数关系式以及定义域.
的函数关系式以及定义域.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若△ABC内一点P满足∠PAC=∠PCB=∠PBA,则称点P为△ABC的布罗卡尔点,三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮.已知△ABC中,CA=CB,∠ACB=120°,P为△ABC的布罗卡尔点,若PA=![]() ,则PB+PC=_____.
,则PB+PC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两组同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示.
(1)直接写出甲组加工零件的数量y与时间x之间的函数关系式;
(2)求乙组加工零件总量a的值;
(3)甲、乙两组加工出的零件合在一起装箱,每满300件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元.
(1)求甲、乙两种型号的机器人每台的价格各是多少万元;
(2)已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件,该公司计划购买这两种型号的机器人共8台,总费用不超过41万元,并且使这8台机器人每小时分拣快递件数总和不少于8300件,则该公司有哪几种购买方案?哪个方案费用最低,最低费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.
(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学在一次测验中解答的填空题:
①若![]() ,则
,则![]() ;
;
②方程![]() 的解为
的解为![]()
③已知三角形两边分别为2和9,第三边长是方程![]() 的根,则这个三角形的周长是17或19。
的根,则这个三角形的周长是17或19。
其中答案完全正确的题目个数是_____个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com