
 函数y=ax2+bx+c与y=kx的图象如图所示,有以下结论:①b2-4ac>0;②a+b+c=k;③方程ax2+bx+c=kx一定有两个不相等的实数根;④当1<x<3时,ax2+(b-k)x+c<0其中正确的个数为( )
函数y=ax2+bx+c与y=kx的图象如图所示,有以下结论:①b2-4ac>0;②a+b+c=k;③方程ax2+bx+c=kx一定有两个不相等的实数根;④当1<x<3时,ax2+(b-k)x+c<0其中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据二次函数图象与系数的关系:抛物线与x轴交点个数与△=b2-4ac的关系、抛物线与直线的交点的坐标与函数解析式的关系、当x=1是两个函数的函数值的关系、函数图象与其解析式及对应不等式的关系逐一分析4个选项.
解答 解:(1)∵抛物线与x轴没有交点,
∴△=b2-4ac<0
故:选项①错误
(2)由图象可知,抛物线与直线有一个交点的横坐标为1,
即:当x=1时,y抛=a+b+c,y直线=k
则:a+b+c=k
故:选项②正确.
(3)∵抛物线与直线有两个交点,
∴方程组$\left\{\begin{array}{l}{y=ax2+bx+c}\\{y=kx}\end{array}\right.$有两组不相等的实数解
∴方程ax2+bx+c=kx一定有两个不相等的实数根;
故:选项③正确
(4)∵ax2+(b-k)x+c<0
∴ax2+bx+c<kx
∵当1<x<3时,函数y=ax2+bx+c的函数值小于函数y=kx的函数值
∴当1<x<3时,ax2+bx+c<kx
即:当1<x<3时,ax2+(b-k)x+c<0
故:选项④正确.
故:选C
点评 本题考查了:二次函数图象与系数的关系、根的判别式,解题的关键是掌握函数图象与系数的关系及两个函数的交点与方程组的关系、函数值的大小与不等式的关系.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
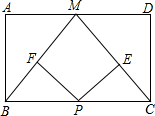 如图,点M是矩形ABCD的边AD的中点,点P为BC上一点,PE⊥MC于点E,PF⊥MB于点F,当AB,BC满足什么条件时,四边形PEMF为矩形.
如图,点M是矩形ABCD的边AD的中点,点P为BC上一点,PE⊥MC于点E,PF⊥MB于点F,当AB,BC满足什么条件时,四边形PEMF为矩形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲班 | B. | 乙班 | C. | 两班一样整齐 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
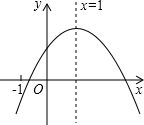 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( )| A. | b>0 | B. | 2a+b=0 | C. | b2-4ac>0 | D. | a-b+c>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com