
类比、转化、分类讨论等思想方法和数学基本图形在数学学习和解题中经常用到,如下是一个案例,请补充完整。
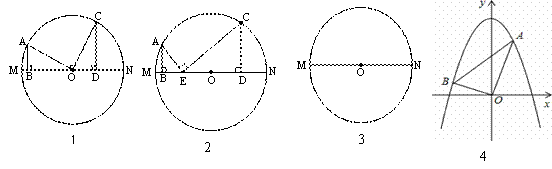
原题:如图1,在⊙O中,MN是直径,AB⊥MN于点B,CD⊥MN于点D,∠AOC=90°,AB=3,CD=4,则BD= 。
⑴尝试探究:如图2,在⊙O中,MN是直径,AB⊥MN于点B,CD⊥MN于点D,点E在MN上,∠AEC=90°,AB=3,BD=8,BE:DE=1:3,则CD= (试写出解答过程)。
⑵类比延伸:利用图3,再探究,当A、C两点分别在直径MN两侧,且AB≠CD,AB⊥MN于点B,CD⊥MN于点D,∠AOC=90°时,则线段AB、CD、BD满足的数量关系为 。
 ⑶拓展迁移:如图4,在平面直角坐标系中,抛物线经过A(m,6),B(n,1)两点(其中0<m<3),且以y轴为对称轴,且∠AOB=90°,①求mn的值;②求抛物线的解析式。
⑶拓展迁移:如图4,在平面直角坐标系中,抛物线经过A(m,6),B(n,1)两点(其中0<m<3),且以y轴为对称轴,且∠AOB=90°,①求mn的值;②求抛物线的解析式。
解:原题:∵AB⊥MN,CD⊥MN,
∴∠ABO=∠ODC=90° ∠BAO+∠AOB=90°
∵∠AOC=90° ∴∠DOC+∠AOB=90°
∴∠BAO=∠DOC 又∵OA=OC ∴△AOB≌△ODC(AAS)
∴OD=AB=3,OB=CD=4,∴BD=OB+OD=7
 |
尝试探究:∵AB⊥MN,CD⊥MN,∴∠ABE=∠CDE=90°
∠BAE+∠AEB=90°∵∠AEC=90°∴∠DEC+∠AEB=90°
∴∠BAE=∠DEC ∴△ABE∽△EDC
∴
∵AB=3,BD=8,BE:DE=1:3,
∴BE=2,DE=6 ∴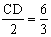 ∴CD=4
∴CD=4
⑵类比延伸:
如图3(a)CD=AB+BD;
 如图3(b)AB=CD+BD
如图3(b)AB=CD+BD
 |
⑶拓展迁移:
① 作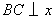 轴于C点,
轴于C点,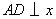 轴于D点,
轴于D点,
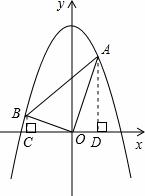
 点坐标分别为
点坐标分别为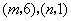 ,
,
∴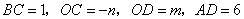 ,又∵∠AOB=90°
,又∵∠AOB=90°
∴∠BCO=∠ODA=90°,∠OBC=∠AOD
∴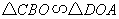 ,
,
∴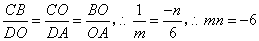 。
。
②由①得,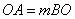 ,又
,又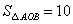 ,∴
,∴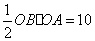 ,
,
即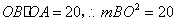 ,
,
又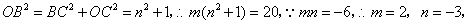
∴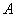 坐标为(2,6),B坐标为(-3,1),
坐标为(2,6),B坐标为(-3,1),
代入得抛物线解析式为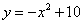


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
)为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.
| 采购数量(件) | 1 | 2 | … |
| A产品单价(元/件) | 1480 | 1460 | … |
| B产品单价(元/件) | 1290 | 1280 | … |
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的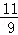 ,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
将二次函数 的图象先向右平移一个单位,再沿x轴翻折到第一象限,然后向右平移一个单位,再沿y轴翻折到第二象限…以此类推,如果把向右平移一个单位再沿坐标轴翻折一次记作1次变换,那么二次函数
的图象先向右平移一个单位,再沿x轴翻折到第一象限,然后向右平移一个单位,再沿y轴翻折到第二象限…以此类推,如果把向右平移一个单位再沿坐标轴翻折一次记作1次变换,那么二次函数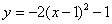 的图象经过2013次变换后,得到的图象的函数解析式为 .
的图象经过2013次变换后,得到的图象的函数解析式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线
 交于A,B两点,且A点在y轴左侧,P点坐标为(0,-4),
交于A,B两点,且A点在y轴左侧,P点坐标为(0,-4),
连接PA,PB.以下说法正确的是( )
① 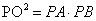 ;② 当k>0时,(PA+AO)(PB-BO)的值随k的增大而增大;③ 当
;② 当k>0时,(PA+AO)(PB-BO)的值随k的增大而增大;③ 当 时,
时,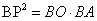 ;④三角形PAB面积的最小值为
;④三角形PAB面积的最小值为 .
.
 A.③④ B.①②
A.③④ B.①② C.②④ D.①④
C.②④ D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1所示,直角梯形OABC的顶点A、C分别在y轴正半轴与 轴负半轴上.过点B、C作直线
轴负半轴上.过点B、C作直线 .将直线
.将直线 平移,平移后的直线
平移,平移后的直线 与
与 轴交于点D,与
轴交于点D,与 轴交于点E.
轴交于点E.
(1)将直线 向右平移,设平移距离CD为
向右平移,设平移距离CD为 (t
(t 0),直角梯形OABC被直线
0),直角梯形OABC被直线 扫过的面积(图中阴影部份)为
扫过的面积(图中阴影部份)为 ,
, 关于
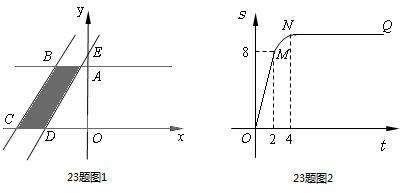
关于 的函数图象如图2所示, OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
的函数图象如图2所示, OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
①求梯形上底AB的长及直角梯形OABC的面积; ②求S关于 的函数解析式;
的函数解析式;
(2)在第(1)题的条件下,当直线 向左或向右平移时(包括
向左或向右平移时(包括 与直线BC重合),在直线AB上是否存在点P,使
与直线BC重合),在直线AB上是否存在点P,使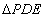 为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com