
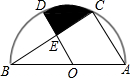
 如图,半圆O中,AB为直径,AB=4,C、D为半圆上两点,四边形OACD为菱形,连接BC交OD于点E,则阴影部分面积为$\frac{2}{3}$π-$\frac{\sqrt{3}}{2}$.
如图,半圆O中,AB为直径,AB=4,C、D为半圆上两点,四边形OACD为菱形,连接BC交OD于点E,则阴影部分面积为$\frac{2}{3}$π-$\frac{\sqrt{3}}{2}$. 分析 此题可用锐角三角函数先求出BE、EO的值,进而用扇形的面积公式及三角形的面积公式即可求出阴影部分的面积.
解答 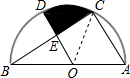 解:∵AB=4,
解:∵AB=4,
∴AO=BO=2,
连接OC,
∵四边形OACD为菱形,
∴AO=AC,
∴△AOC是等边三角形,
∴∠A=∠BOE=60°,
∴∠COD=60°,
∵AB为直径,
∴∠ACB=90°,
∴∠B=30°,
∴BC⊥OD,
∴BE=CE=$\sqrt{3}$,
∴OE=$\frac{1}{2}$AC=1,
∴S阴影=S扇形OCD-S△CEO=$\frac{60•π×{2}^{2}}{360}$-$\frac{1}{2}$×$\sqrt{3}$×1=$\frac{2}{3}$π-$\frac{\sqrt{3}}{2}$,
故答案为:$\frac{2}{3}$π-$\frac{\sqrt{3}}{2}$.
点评 本题主要考查解直角三角形、扇形和三角形的面积公式,解题的关键是看出S阴影=S扇形COD-S△CEO.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:解答题
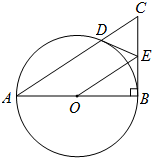 如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE,OE.
如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE,OE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
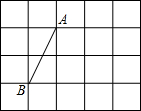 如图,A、B两点均在由小正方形组成的网格格点上,若C点也在格点上,且△ABC是等腰直角三角形,则符合条件的C点的个数有( )
如图,A、B两点均在由小正方形组成的网格格点上,若C点也在格点上,且△ABC是等腰直角三角形,则符合条件的C点的个数有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
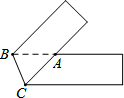 将一张宽为5cm的长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,则这个三角形面积的最小值是$\frac{25}{2}$cm2.
将一张宽为5cm的长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,则这个三角形面积的最小值是$\frac{25}{2}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 钝角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com