
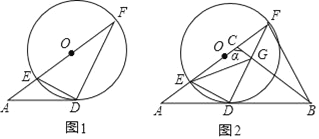
【题目】如图:AD与⊙O相切于点D,AF经过圆心与圆交于点E、F,连接DE、DF,且EF=6,AD=4.
(1)证明:AD2=AEAF;
(2)延长AD到点B,使DB=AD,直径EF上有一动点C,连接CB交DF于点G,连接EG,设∠ACB=α,BG=x,EG=y.
①当α=900时,探索EG与BD的大小关系?并说明理由;
②当α=1200时,求y与x的关系式,并用x的代数式表示y.
【答案】(1)证明见解析;(2)①当α=90°时,EG>BD,理由见解析;②当α=120°时,y=![]() .
.
【解析】试题分析:(1)连接OD,由AD是⊙O的切线,根据切线的性质可得OD⊥AD,即∠ADE+∠EDO=90°,再由EF是直径,根据圆周角定理的推论可得∠EDF=90°,即∠EDO+∠ODF=90°,即可得∠ADE=∠ODF,再由OD=OF,根据等腰三角形的性质可得∠ODF=∠OFD,所以∠ADE=∠OFD,即可判定△ADE∽△AFD,根据相似三角形的性质可得![]() ,即AD2=AEAF;(2)①当α=90°时,EG>BD,理由如下:取EG的中点H,连接CH、DH、CD,在Rt△EDG、Rt△ECG中,点H为EG的中点,根据直角三角形斜边的中线等于斜边的一半可得CH=EH=GH=DH=
,即AD2=AEAF;(2)①当α=90°时,EG>BD,理由如下:取EG的中点H,连接CH、DH、CD,在Rt△EDG、Rt△ECG中,点H为EG的中点,根据直角三角形斜边的中线等于斜边的一半可得CH=EH=GH=DH=![]() EG,根据圆的定义即可判定点C、E、D、G在以点H为圆心,EG为直径的圆上,根据直径是圆中最长的弦可得EG>CD,在Rt△ABC中,DB=AD,再由直角三角形斜边的中线等于斜边的一半可得CD= DB=AD=
EG,根据圆的定义即可判定点C、E、D、G在以点H为圆心,EG为直径的圆上,根据直径是圆中最长的弦可得EG>CD,在Rt△ABC中,DB=AD,再由直角三角形斜边的中线等于斜边的一半可得CD= DB=AD=![]() AB,即可得结论EG>BD;②当α=120°时,将△ADE绕着点D旋转180°,得到△BDP,连接GP,由(1)AD2=AEAF可得16=AE(AE+6),解得AE=2或AE=-8(舍去),因△ADE≌△BDP,根据全等三角形的性质可得ED=DP,AE=BP=2,∠A=∠DBP,再由∠EDF=90°可得DG垂直平分EP,根据线段垂直平分线的性质可得GE=GP=y,因∠A+∠ABC=180°-120°=60°所以∠DBP+∠ABC=60°,即∠GBP=60°;过点P作PQ⊥BG,在Rt△BPQ中,∠GBP=60°,BP=2,可求得BQ=1,PQ=
AB,即可得结论EG>BD;②当α=120°时,将△ADE绕着点D旋转180°,得到△BDP,连接GP,由(1)AD2=AEAF可得16=AE(AE+6),解得AE=2或AE=-8(舍去),因△ADE≌△BDP,根据全等三角形的性质可得ED=DP,AE=BP=2,∠A=∠DBP,再由∠EDF=90°可得DG垂直平分EP,根据线段垂直平分线的性质可得GE=GP=y,因∠A+∠ABC=180°-120°=60°所以∠DBP+∠ABC=60°,即∠GBP=60°;过点P作PQ⊥BG,在Rt△BPQ中,∠GBP=60°,BP=2,可求得BQ=1,PQ=![]() ,所以GQ=BG-BQ=x-1,在Rt△GPQ中, PQ=
,所以GQ=BG-BQ=x-1,在Rt△GPQ中, PQ=![]() ,GQ=x-1,GP=y,由勾股定理可得PG2=GQ2+PQ2,即y2=(x-1) 2+(
,GQ=x-1,GP=y,由勾股定理可得PG2=GQ2+PQ2,即y2=(x-1) 2+(![]() ) 2 ,整理即可得y=
) 2 ,整理即可得y=![]() .
.
试题解析:
(1)证明:连接OD
∵AD是⊙O的切线
∴OD⊥AD,即∠ADE+∠EDO=90°
∵EF是直径

∴∠EDF=90°,即∠EDO+∠ODF=90°
∴∠ADE=∠ODF
∵OD=OF
∴∠ODF=∠OFD
∴∠ADE=∠OFD
∴△ADE∽△AFD
∴![]() ,即
,即![]()
(2)①当![]() 时,EG>BD
时,EG>BD
理由如下:取EG的中点H,连接CH、DH、CD,
∵Rt△EDG、Rt△ECG,点H为EG的中点
∴CH=EH=GH=DH= ![]()
∴点C、E、D、G在以点H为圆心,EG为直径的圆上
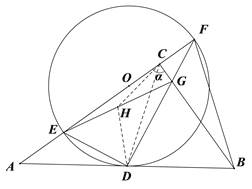
∴EG>CD
∵Rt△ABC, DB=AD
∴CD= DB=AD= ![]()
∴EG>BD
②当![]() 时
时
将△ADE绕着点D旋转180°,得到△BDP,连接GP
由(1)![]() 得:
得: ![]() ,解得AE=2或AE=-8(舍去)
,解得AE=2或AE=-8(舍去)
∴△ADE≌△BDP
∴ED=DP,AE=BP=2,∠A=∠DBP
∵∠EDF=90°
∴DG垂直平分EP
∴GE=GP= ![]()
∵∠A+∠ABC=180°-120°=60°
∴∠DBP+∠ABC=60°,即∠GBP=60°
过点P作PQ⊥BG
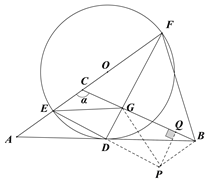
在Rt△BPQ中,∠GBP=60°,BP=2
∴BQ=1,PQ=![]()
∴GQ=BG-BQ= ![]() -1
-1
在Rt△GPQ中, PQ=![]() ,GQ=
,GQ= ![]() -1,GP=
-1,GP= ![]()
∴![]()
即![]()
![]()


科目:初中数学 来源: 题型:
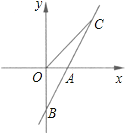
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
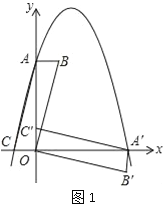
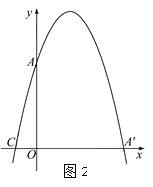
【题目】在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(﹣1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
(1)若抛物线经过点C、A、A′,求此抛物线的解析式;
(2)点M时第一象限内抛物线上的一动点,问:当点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时M的坐标;
(3)若P为抛物线上一动点,N为x轴上的一动点,点Q坐标为(1,0),当P、N、B、Q构成平行四边形时,求点P的坐标,当这个平行四边形为矩形时,求点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】坐标平面上的点P(2,﹣1)向上平移2个单位,再向左平移1个单位后,点P的坐标变为( )
A.(2,1)B.(﹣2,1)C.(1,1)D.(4,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
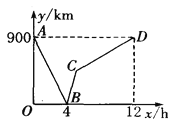
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x h,两车之间的距离为y km,如图所示的折线表示y与x之间的函数关系.根据图象进行以下探究:
(1)甲、乙两地之间的距离为_______km;
(2)请解释图中点B的实际意义;
(3)求慢车和快车的速度;
(4)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC的顶点分别为A(-4, 5),B(﹣3, 2),C(4,-1).
⑴作出△ABC关于x轴对称的图形△A1B1C1;
⑵写出A1、B1、C1的坐标;
⑶若AC=10,求△ABC的AC边上的高.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
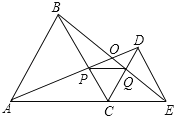
【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有 .(把你认为正确的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com