
����Ŀ����ͼ��������ABCD��һ�κ���y��x+1ͼ�������һ�����������Σ�
��1����ij������һ�κ���y��x+1��������ͼ������а��������εı߳���

��2����ij�����Ƿ���������![]() ������ͼ��İ���������ΪABCD����D��2��m����m��2���ڷ���������ͼ���ϣ���m��ֵ����������������ʽ��
������ͼ��İ���������ΪABCD����D��2��m����m��2���ڷ���������ͼ���ϣ���m��ֵ����������������ʽ��

��3����ij�����Ƕ��κ���y��ax2+c��a��0��������ͼ��İ���������ΪABCD��C��D�е�һ��������Ϊ��3��4����д���������������������ϵ���һ���������꣬д���������������һ�������߽���ʽ�����ж���д���������ߵİ��������εĸ�������������ż����������С��ֻ��ֱ��д���𰸣�

���𰸡���1�������α߳�Ϊ![]() ����2��m��1��y��
����2��m��1��y��![]() ����3��D��������1��3����y��
����3��D��������1��3����y��![]() x2+
x2+ ![]() ��������κ������ߵİ��������θ���Ϊż����
��������κ������ߵİ��������θ���Ϊż����
��������
�����Ϊ��ӱ���ر�Ҫע������ͷ������⣬���İ�����֪꣬A��BΪ�����������㣬C��DΪ����ͼ���ϵ����㣺��1������ȷ�ػ���ͼ�Σ������������ε�����ȷ����ص������Ӷ����������εı߳���ע��˼ά�������ԣ�
��2����ΪABCDΪ�����Σ����Կ������ߵõ�����ֱ�������Σ����õ�D��2��m���������ʾ����C������Ӷ���⣮
��3��ע��˼ά�������ԣ������߿��ڼȿ������ϣ�Ҳ�������£��������߿�������ʱ�������ε���һ������Ҳ�����������ϣ������ȿ����ڵ㣨3��4������ߣ�Ҳ�����ڵ㣨3��4�����ұߣ����㣨3��4����x�������ߣ�����ȫ��������ȷ���߶εij�����ȷ������������һ��������ꣻ�������߿�������ʱҲ��һ���ط�Ϊ������������ۣ�
��1����������ABCD��һ�κ���y��x+1ͼ�������һ�����������Σ�
����A��x�������ᡢ��B��y�Ḻ������ʱ��
��AO��1��BO��1��
��������ABCD�ı߳�Ϊ![]()
����A��x�Ḻ���ᡢ��B��y����������ʱ����������ABCD�ı߳�Ϊa����3a��![]()
��a=![]()
![]() ,���������α߳�Ϊ
,���������α߳�Ϊ![]()
![]() ��
��
��2����DE��CF�ֱ�ֱ��x��y�ᣬ
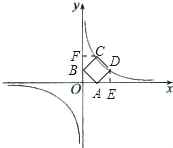
֪��ADE�ա�BAO�ա�CBF����ʱ��m��2��DE��OA��BF��m��OB��CF��AE��2��m
��OF��BF+OB��2
��C��������2��m��2��
��2m��2��2��m��
���m��1��
�෴���������Ľ���ʽΪy��![]() ��
��
��3���������⻭��ͼ�Σ���ͼ��ʾ��
��C��CF��x�ᣬ����ΪF����D��DE��CF������ΪE��
���CED�ա�DGB�ա�AOB�ա�AFC��
��C��3��4������CF��4��OF��3��
��EG��3��DE��4����DG��DE��GE��DE��OF��4��3��1����D����Ϊ����1��3�������D��C�������ߵĽ���ʽΪ��y��ax2+b��
��D��C���������ã�![]() ��
��
���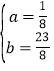 ��
��
����������������ߵĽ���ʽΪy��![]() x2+
x2+![]() ��
��
ͬ���ɵ�D���������Ϊ����7����3��������4��7������4��1������Ӧ�������߷ֱ�Ϊy=![]() x2+
x2+![]() ��y=
��y=![]() x2+
x2+![]() ��y=
��y=![]() x2+
x2+![]() ��������κ������ߵİ��������θ���Ϊż����
��������κ������ߵİ��������θ���Ϊż����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ҽ�ί�涨����Сѧ��ÿ����У�����ʱ�䲻����1Сʱ����Ϊ��ij��ѧΪ���˽�ѧ���������������������720����ҵ��ѧ�������������ǣ���ÿ������Ƿ�1Сʱ��δ����1Сʱ��ԭ���������õ������Ƴ��˵�����ͳ��ͼ��Ƶ���ֲ�ֱ��ͼ������ͼʾ������������⣺
��1�����ڱ������ѧ�������ѡ��һ��ѧ�������������ɼ���ѡ����ǡ������ÿ���������1Сʱ����ѧ���ĸ����Ƕ��٣�
��2����ûʱ�����������Ƕ��٣�����ȫƵ���ֲ�ֱ��ͼ��
��3��2010������������б�ҵ��ԼΪ3.2���ˣ����˵��飬���Թ���2010������������б�ҵ����ÿ�����δ����1Сʱ��ѧ��Լ�ж������ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12�֣���ͼ����֪������ABC�ı�AB����O�����ߣ��е�ΪB��AC����Բ��O����Բ�ཻ�ڵ�D��C����C��ֱ��CE�AAB����AB���ӳ����ڵ�E��

��1����֤��CBƽ����ACE��
��2����BE=3��CE=4������O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У�BC��12����AD��8������EFGH��һ��GH��BC�ϣ�����E��F�ֱ���AB��AC�ϣ�AD��EF���ڵ�M��
��1����֤��![]() ��
��
��2����EF��x��EH��y��д��y��x֮��ĺ�������ʽ��
��3�������EFGH�����ΪS����S��x֮��ĺ�������ʽ����д��S�����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
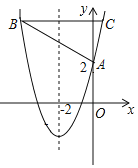
����Ŀ����ͼ��������y=x2+bx+c��y�ύ�ڵ�A��0��2�����Գ���Ϊֱ��x=��2��ƽ����x���ֱ���������߽���B��C���㣬��B�ڶԳ�����࣬BC=6��
��1����������ߵĽ���ʽ��
��2����P��x���ϣ�ֱ��CP����ABC����ֳ�2��3�����֣���ֱ��д��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������y��ax2+bx+c�ĶԳ�����x����1����x���һ������Ϊ(��5��0)����һԪ���η���ax2+bx+c��0����һ��Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
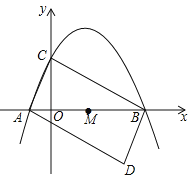
����Ŀ����ͼ��������y=��![]() x2+
x2+![]() x+2��x�ύ�ڵ�A��B����y�ύ�ڵ�C��
x+2��x�ύ�ڵ�A��B����y�ύ�ڵ�C��
��1������A��B��C�����ꣻ
��2������ABC��AB�е�M��ת180�㣬�õ���BAD��3
�����D�����ꣻ
���ж��ı���ADBC����״����˵�����ɣ�
��3���ڸ������߶Գ������Ƿ���ڵ�P��ʹ��BMP����BAD���ƣ������ڣ���ֱ��д����������������P������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
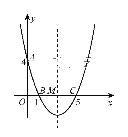
����Ŀ����ͼ,��ֱ������ϵ��,�����߾�����A(0,4),B(1,0),C(5,0),��Գ�����x���ཻ�ڵ�M.
(1)�������ߵĽ���ʽ�ͶԳ���;
(2)�������ߵĶԳ������Ƿ����һ��P,ʹ��PAB���ܳ���С?������,�������P������;��������,��˵������;
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������x�ķ��̣�mx2����3m��1��x+2m��2=0��
��1����֤������mȡ��ֵʱ�����̺���ʵ������
��2��������x�Ķ��κ���y=mx2����3m��1��x+2m��2��ͼ����x���������ľ���Ϊ2ʱ���������ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com