
如下图所示,在边长为100米的正三角形路上,有甲、乙二人分别从两个不同的顶点处,按逆时针方向同时出发,甲速度为4米/秒,乙速度为3米/秒.问出发多长时间,甲、乙二人第一次走在同一条边上?

|
解:分两种情况讨论: (1)若开始时甲在C处,乙在A处. 已知甲速>乙速,那么当甲走完AC边100米进入AB边时,乙还没有离开AB边. 而甲走100米需100÷4=25(秒), 即在这种情况下,出发25秒后,甲、乙二人第一次走在同一条边上. (2)若开始时甲在A处,乙在C处. 设甲经过x秒后追赶乙至正三角形的同一边上,则x需满足 0≤200-(4x-3x)≤100, 即100≤x≤200. 当x=100时,乙的路程为3×100=300(米),说明乙又到了点C. 而此时甲的路程为4×100=400(米),说明甲到了点B,点B和C在同一边BC上,所以在这种情况下,出发100秒后,甲、乙二人第一次走在同一条边上. 分析:由题意,知甲、乙有两种可能位置:(1)甲在乙后100米;(2)甲在乙后200米. 注意:本例第二种情况的连续不等式非常重要,忽略任何一边都不完整,所以对应用题一定要考虑周全. |


科目:初中数学 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:022
如下图所示,在边长为4的正方形内部,以各边为直径分别作4个半圆,则图中阴影部分的面积是________.
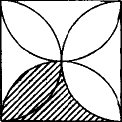
查看答案和解析>>
科目:初中数学 来源:2007年陕西省初中毕业生学业考试数学模拟试卷(八) 题型:013
如下图所示,在边长为a的正方形中挖去一个边长为b的小正方形(a>b),再把剩余的部分剪拼成一个矩形,通过计算图形(阴影部分)的面积,验证了一个等式是
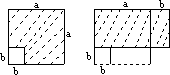
A.a2-b2=(a+b)(a-b)
B.(a-b)2=a2+2ab+b2
C.(a-b)2=a2-2ab+b2
D.(a+2b)(a-b)=a2+ab-2b2
查看答案和解析>>
科目:初中数学 来源:江苏期中题 题型:解答题



查看答案和解析>>
科目:初中数学 来源:江苏期中题 题型:解答题



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com