

分析 根据题意,作辅助线BE⊥AD于点E,构造出直角三角形,由题目中的信息可以得到DE的长,BC=DE,从而得到BC的长,本题得以解决.
解答 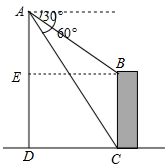 解:作BE⊥AD于点E,如右图所示,
解:作BE⊥AD于点E,如右图所示,
由已知可得,
∠ACD=60°,∠AEB=∠ADC=90°,∠ABE=30°,AD=420米,
∴BE=$\frac{AE}{sin30°}$,CD=$\frac{AD}{sin60°}$,
∵BE=CD,
∴$\frac{AE}{sin30°}=\frac{AD}{sin60°}$,
即$\frac{AE}{\frac{1}{2}}=\frac{420}{\frac{\sqrt{3}}{2}}$,
解得,AE=140$\sqrt{3}$,
∴DE=AD-AE=420-140$\sqrt{3}$≈178米,
∵BC=DE,
∴BC=178米,
即“河南大玉米”的高度约为178米.
点评 本题考查解直角三角形的应用-仰角俯角问题,解题的关键是明确题意,构造合适的直角三角形,利用数形结合的思想解答,注意最后结果要精确到1m.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:选择题
 将一组整数按如图所示的规律排列下去,若有序数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示的数为8,则(7,4)表示的数是( )
将一组整数按如图所示的规律排列下去,若有序数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示的数为8,则(7,4)表示的数是( )| A. | 32 | B. | 24 | C. | 25 | D. | -25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
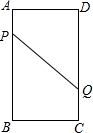 A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别从A、C同时出发,点P以3厘米每秒的速度向点B移动,一直到达点B为止,点Q以2厘米每秒的速度向点D移动.
A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别从A、C同时出发,点P以3厘米每秒的速度向点B移动,一直到达点B为止,点Q以2厘米每秒的速度向点D移动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com