
【题目】已知:把Rt△ABC和Rt△DEF按如图1摆放(点C与点E重合),点B、C(E)、F在同一条直线上,∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=9cm,如图2,△DEF从图1的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).解答下列问题:
(1)用含t的代数式表示线段AP= ;
(2)当t为何值时,点E在∠A的平分线上?
(3)当t为何值时,点A在线段PQ的垂直平分线上?
(4)连接PE,当t=1(s)时,求四边形APEC的面积.

【答案】(1)(10﹣2t)cm.(2)![]() ;(3)t=2;(4)20
;(3)t=2;(4)20
【解析】
(1)利用勾股定理求出AB,根据AP=AB﹣BP计算即可.
(2)如图1中,作AT平分∠BAC,作TH⊥AB于H.设TC=TH=x,证明Rt△ATH≌Rt△ATC(HL),推出AH=AC=8,在Rt△BTH中,则有(6﹣x)2=22+x2,求出x即可解决问题.
(3)根据线段垂直平分线的性质得到AP=AQ,根据等腰三角形的性质得到CE=CQ,根据勾股定理求出AB,列式计算即可.
(4)作PM⊥BE交BE于M,根据S四边形APEC=S△ABC﹣S△BPE计算算即可.
(1)在Rt△ABC中,∵∠ACB=90°,AC=8cm,BC=6cm,
∴AB=![]() =
=![]() =10(cm),
=10(cm),
由题意PA=AB﹣BP=(10﹣2t)cm,
故答案为(10﹣2t)cm.
(2)如图1中,作AT平分∠BAC,作TH⊥AB于H.
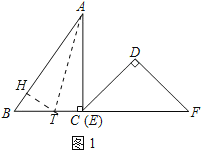
∵TC⊥AC,TH⊥AB,TA平分∠ABC,
∴TC=TH,∠AHT=∠ACT=90°,设TC=TH=x,
∵AT=AT,
∴Rt△ATH≌Rt△ATC(HL),
∴AH=AC=8,
∴BH=AB﹣AH=10﹣8=2,
在Rt△BTH中,则有(6﹣x)2=22+x2,
解得x=![]() ,
,
∴当t为![]() 时,点E在∠A的平分线上.
时,点E在∠A的平分线上.
(3)∵点A在线段PQ的垂直平分线上,
∴AP=AQ,
∵∠DEF=45°,∠ACB=90°,∠DEF+∠ACB+∠EQC=180°,
∴∠EQC=45°,
∴∠DEF=∠EQC,
∴CE=CQ,
由题意知:CE=t,BP=2t,
∴CQ=t,
∴AQ=8﹣t,
在Rt△ABC中,由勾股定理得,AB=10cm,
则AP=10﹣2t,
∴10﹣2t=8﹣t,
解得:t=2,
答:当t=2s时,点A在线段PQ的垂直平分线上;
(4)如图2中,过P作PM⊥BE,交BE于M,

∴∠BMP=90°,
在Rt△ABC和Rt△BPM中,sinB=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得,PM=![]() ,
,
∵BC=6cm,CE=t,
∴BE=6﹣1=5,
∴S四边形APEC=S△ABC﹣S△BPE=![]() ×BC×AC﹣
×BC×AC﹣![]() ×BE×PM=
×BE×PM=![]() ×6×8﹣
×6×8﹣![]() ×5×
×5×![]() =20.
=20.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,BC=7,点E是AD上的一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD的平分线上时,CA1的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=60°,AD平分∠BAC,CE平分∠BCA,AD、CE交于点F,CD=CG,连结FG.

(1)求证:FD=FG;
(2)线段FG与FE之间有怎样的数量关系,请说明理由;
(3)若∠B≠60°,其他条件不变,则(1)和(2)中的结论是否仍然成立?请直接写出判断结果,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某歌星演唱会票价如下:甲种票每张200元,乙种票每张100元.工会小组准备了1000元,全部用来买票,且每种至少买一张.
(1)共有多少种购票方案?列举出所有可能结果;
(2)如果从上述方案中任意选中一种方案购票,求恰好买到7张门票的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2002年国际数学家大会在北京召开,大会选用了赵爽弦图作为会标的中心图案.如图,由四个全等的直角三角形与一个小正方形拼成一个大正方形.如果大正方形的面积是25,直角三角形较长的直角边长是a,较短的直角边长是b,且(a+b)2的值为49,那么小正方形的面积是( )

A.2B.0.5C.13D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盐阜人民商场经营某种品牌的服装,购进时的单价是![]() 元,根据市场调查:在一段时间内,销售单价是
元,根据市场调查:在一段时间内,销售单价是![]() 元时,销售量是
元时,销售量是![]() 件,而销售单价每涨
件,而销售单价每涨![]() 元,就会少售出
元,就会少售出![]() 件服装.
件服装.
![]() 设该种品牌服装的销售单价为
设该种品牌服装的销售单价为![]() 元
元![]() ,销售量为
,销售量为![]() 件,请写出
件,请写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 若商场获得了
若商场获得了![]() 元销售利润,该服装销售单价
元销售利润,该服装销售单价![]() 应定为多少元?
应定为多少元?
![]() 在
在![]() 问条件下,若该商场要完成不少于
问条件下,若该商场要完成不少于![]() 件的销售任务,求商场销售该品牌服装获得的最大利润是多少?
件的销售任务,求商场销售该品牌服装获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点.现从点
的中点.现从点![]() 观察线段
观察线段![]() ,当长度为
,当长度为![]() 的线段
的线段![]() (图中的黑粗线)以每秒
(图中的黑粗线)以每秒![]() 个单位长的速度沿线段
个单位长的速度沿线段![]() 从左向右运动时,
从左向右运动时,![]() 将阻挡部分观察视线,在
将阻挡部分观察视线,在![]() 区域内形成盲区.设
区域内形成盲区.设![]() 的左端点从
的左端点从![]() 点开始,运动时间为
点开始,运动时间为![]() 秒
秒![]() .设
.设![]() 区域内的盲区面积为
区域内的盲区面积为![]() (平方单位).
(平方单位).

![]() 求
求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 请简单概括
请简单概括![]() 随
随![]() 的变化而变化的情况.
的变化而变化的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师出示了小黑板上的题后(如图),小华说:过点(3,0);小彬说:过点(4,3);小明说:a=1;小颖说:抛物线被x轴截得的线段长为2.你认为四人的说法中,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C 是线段 AB 上一点,且△ACD 和△BCE 都是等边三角形,连接 AE、BD 相交于点 O,AE、BD 分别交 CD、CE 于 M、N,连接 MN、OC,则下列所给的结论中:①AE=BD;②CM=CN;③MN∥AB;④∠AOB=120;⑤OC 平分∠AOB.其中结论正确的个数是( )

A.2B.3C.4D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com