练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．如图，小明用自制的直角三角形纸板DEF测量树AB的高度，测量时，使直角边DF保持水平状态，其延长线交AB于点G；使斜边DE所在的直线经过点A．测得边DF离地面的高度为1m，点D到AB的距离等于7.5m．已知DF=1.5m，EF=0.6m，那么树AB的高度等于（　　）
    A．4mB．4.5mC．4.6mD．4.8m

    分析 先证明△DEF∽△DAB，利用相似比计算出AG，然后计算AG+GB即可得到AB的长．

    解答 解：如图，BG=DC=1m，DG=7.5m，
    ∵EF∥AG，
    ∴△DEF∽△DAB，
    ∴$\frac{EF}{AG}$=$\frac{DF}{DG}$，即$\frac{0.6}{AG}$=$\frac{1.5}{7.5}$，
    ∴AG=3，
    ∴AB=BG+AG=1+3=4（m）．
    故选A．

    点评 本题考查了相似三角形的应用：利用影长测量物体的高度；利用相似测量河的宽度（测量距离）；借助标杆或直尺测量物体的高度．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    6．如图，直线AB∥CD，直线EF分别交AB、CD于点E、F，若∠AEF=50°，则∠EFC的度数是130°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．化简：（25+4$\sqrt{3}$）0-（-1）2012+|-$\sqrt{5}$|=$\sqrt{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

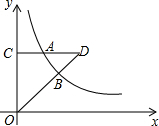    4．如图，A，B是反比例函数y=$\frac{k}{x}$（k＞0，x＞0）图象上两点，AC⊥y轴于C，CA交OB于D，已知$\frac{BD}{OB}$=$\frac{1}{2}$，S四边形OBAC=11，则k=12．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如图，跷跷板AB的支柱OD经过它的中点O，且垂直于地面BC，垂足为D，OD=50cm，当它的一端B着地时，另一端A离地面的高度AC为100cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．若二次函数y=ax2+bx+c（a≠0）与x轴交于两个不同点A（x1，0），B（x2，0）；且二次函数化为顶点式是y=a（x-h）2+k，则下列说法：
    ①b2-4ac＞0；
    ②x1+x2=2h；
    ③二次函数y=ax2+bx+2c（a≠0）化为顶点式为y=a（x-h）2+2k；
    ④若c=k，则一定有h=b．
    正确的有（　　）
    A．①②B．①②③C．①②④D．①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

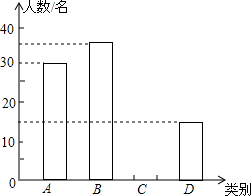    8．由于各地雾霾天气越来越严重，2015年春节前夕，蚌埠市某校团委向全校3000名学生发出“减少空气污染，少放烟花爆竹”倡议书，并围绕“A类：不放烟花爆竹；B类：少放烟花爆竹；C类：不会减少烟花爆竹数量；D类：使用电子鞭炮”四个选项对100名学生进行问卷调查，并将调查结果绘制成如下两幅统计图表（不完整），请根据图表，回答下列问题：
    类别频数频率
    Aam
    B350.35
    C200.20
    Dbn
    合计1001.00
    （1）表格中a=30，b=15，并补全条形统计图；
    （2）如果绘制扇形统计图，请求出C类所占的圆心角的度数；
    （3）根据抽样结果，请估计全校“不放烟花爆竹”或“使用电子鞭炮”的学生有多少名？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知，如图，直线MN交⊙O于A，B两点，AC是⊙O的直径，DE切⊙O于点D，且DE⊥MN于点E．
    （1）求证：AD平分∠CAM．
    （2）若DE=6，AE=3，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．分解因式：mx4-16m=m（x2+4）（x+2）（x-2）．

    查看答案和解析>>

    同步练习册答案