
【题目】如图,已知,EG∥AF,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题。并证明这个命题(只写出一种情况)①AB=AC; ②DE=DF; ③BE=CF。(在已知和求证中,填写正确序号)
已知:EG∥AF,_______,_________.
求证:__________.

科目:初中数学 来源: 题型:
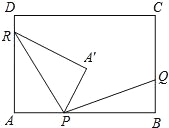
【题目】如图,在矩形ABCD中,AB=8k,BC=5k(k为常数,且k>0),动点P在AB边上(点P不与A、B重合),点Q、R分别在BC、DA边上,且AP:BQ:DR=3:2:1.点A关于直线PR的对称点为A′,连接PA′、RA′、PQ.
(1)若k=4,PA=15,则四边形PARA′的形状是 ;
(2)设DR=x,点B关于直线PQ的对称点为B′点.
①记△PRA′的面积为S1,△PQB′的面积为S2.当S1<S2时,求相应x的取值范围及S2﹣S1的最大值;(用含k的代数式表示)
②在点P的运动过程中,判断点B′能否与点A′重合?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定对居民生活用电实行“阶梯电价”收费,具体收费标准见表:
一户居民一个月用电量的范围 | 电费价格(单位:元/度) |
不超过200度 | a |
超过200度的部分 | b |
已知4月份,该市居民甲用电250度,交电费130元;居民乙用电400度,交电费220元.
(1)求出表中a和b的值;
(2)实行“阶梯电价”收费以后,该市一户居民月用电多少度时,其当月的平均电价每度不超过0.56元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式;
(2)结合图象写出,0<x<4时,直接写出y的取值范围 ;
(3)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.当BC=1时,求出矩形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=﹣![]() +bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣
+bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣![]() +bx+c的图象分别交于B,C两点,点B在第一象限.
+bx+c的图象分别交于B,C两点,点B在第一象限.
(1)求二次函数y=﹣![]() +bx+c的表达式;
+bx+c的表达式;
(2)连接AB,求AB的长;
(3)连接AC,M是线段AC的中点,将点B绕点M旋转180°得到点N,连接AN,CN,判断四边形ABCN的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将多项式x3-5xy2-7y3+8x2y按某一个字母的升幂排列,正确的是()
A. x3-7y3-5xy2+8x2y B. -7y3-5xy2+8x2y+x3 C. 7y3-5xy2+8x2y+x3 D. x3-5xy2+8x2y-7y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年是高安发展史上进位赶超、值得铭记的一年.全年实现生产总值448.78亿元,同比净增29.78亿元.“十全十美、品牌高安”建设迈出更加坚实步伐.数据448.78亿用科学记数法表示为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度).
(1)作出△ABC绕点A顺时针方向旋转90°后得到的△A1B1C1,并直接写出C1点的坐标;
(2)作出△ABC关于原点O成中心对称的△A2B2C2,并直接写出B2的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com