
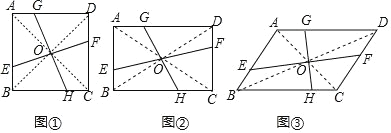
【题目】在四边形 ABCD 中,对角线 AC、BD 相交于点 O,过点 O 的两条直线分别交边 AB、CD、AD、BC 于点 E、F、G、H.
(感知)如图①,若四边形 ABCD 是正方形,且 AG=BE=CH=DF,则 S 四边形AEOG= S 正方形 ABCD;
(拓展)如图②,若四边形 ABCD 是矩形,且 S 四边形 AEOG=![]() S 矩形 ABCD,设 AB=a, AD=b,BE=m,求 AG 的长(用含 a、b、m 的代数式表示);
S 矩形 ABCD,设 AB=a, AD=b,BE=m,求 AG 的长(用含 a、b、m 的代数式表示);
(探究)如图③,若四边形 ABCD 是平行四边形,且 AB=3,AD=5,BE=1, 试确定 F、G、H 的位置,使直线 EF、GH 把四边形 ABCD 的面积四等分.
【答案】【感知】![]() ;【拓展】AG=
;【拓展】AG=![]() ;【探究】当 AG=CH=
;【探究】当 AG=CH=![]() ,BE=DF=1 时,直线 EF、GH 把四边形 ABCD 的面积四等分.
,BE=DF=1 时,直线 EF、GH 把四边形 ABCD 的面积四等分.
【解析】
感知:如图①,根据正方形的性质和全等三角形的性质即可得到结论;
拓展:如图②,过O作ON⊥AD于N,OM⊥AB于M,根据图形的面积得到![]() mb=
mb= ![]() AGa,于是得到结论;
AGa,于是得到结论;
探究:如图③,过O作KL⊥AB,PQ⊥AD,则KL=2OK,PQ=2OQ,根据平行四边形的面积公式得到![]() =
= ![]() ,根据三角形的面积公式列方程即可得到结论.
,根据三角形的面积公式列方程即可得到结论.
感知:如图①,
∵四边形ABCD是正方形,
∴∠OAG=∠OBE=45°,OA=OB,
在△AOG与△BOE中,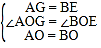 ,
,
∴△AOG≌△BOE,
∴S四边形AEOG=S△AOB=![]() S正方形 ABCD;
S正方形 ABCD;
故答案为:![]() ;
;
拓展:如图②,过O作ON⊥AD于 N,OM⊥AB于M,

∵S△AOB=![]() S矩形ABCD,S四边形AEOG=
S矩形ABCD,S四边形AEOG=![]() S矩形ABCD,
S矩形ABCD,
∴S△AOB=S四边形AEOG,
∵S△AOB=S△BOE+S△AOE,S四边形AEOG=S△AOG+S△AOE,
∴S△BOE=S△AOG,
∵S△BOE=![]() BEOM=
BEOM=![]() m·
m·![]() b=
b=![]() mb,S△AOG=
mb,S△AOG=![]() AGON=
AGON=![]() AG
AG![]() a=
a=![]() AGa,
AGa,
∴![]() mb=
mb=![]() AGa,
AGa,
∴AG=![]() ;
;
探究:如图③,过O作KL⊥AB,PQ⊥AD,

则 KL=2OK,PQ=2OQ,
∵S平行四边形ABCD=ABKL=ADPQ,
∴3×2OK=5×2OQ,
∴![]() =
=![]() ,
,
∵S△AOB=![]() S平行四边形ABCD,S四边形AEOG=
S平行四边形ABCD,S四边形AEOG=![]() S平行四边形ABCD,
S平行四边形ABCD,
∴S△AOB=S四边形AEOG,
∴S△BOE=S△AOG,
∵S△BOE=![]() BEOK=
BEOK=![]() ×1×OK,S△AOG=
×1×OK,S△AOG=![]() AGOQ,
AGOQ,
∴![]() ×1×OK=
×1×OK=![]() AGOQ,
AGOQ,
∴![]() =AG=
=AG=![]() ,
,
∴当AG=CH=![]() ,BE=DF=1时,直线EF、GH把四边形ABCD的面积四等分.
,BE=DF=1时,直线EF、GH把四边形ABCD的面积四等分.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】为调查达州市民上班时最常用的交通工具的情况,随机抽取了部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭汽车,E:其他”五个选项中选择最常用的一项.将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
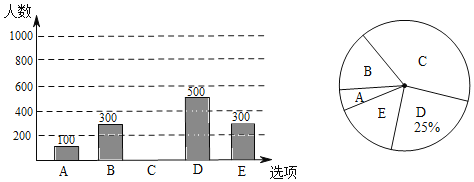
(1)本次调查中,一共调查了 名市民;扇形统计图中,B项对应的扇形圆心角是 度;补全条形统计图;
(2)若甲、乙两人上班时从A,B,C,D四种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人恰好选择同一种交通工具上班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一小球沿与地面成一定角度的方向飞出,小球的飞行路线是一条抛物线,如果不考虑空气阻力,小球的飞行高度y(单位:m)与飞行时间x(单位:s)之间具有函数关系y=﹣5x2+20x,请根据要求解答下列问题:
(1)在飞行过程中,当小球的飞行高度为15m时,飞行时间是多少?
(2)在飞行过程中,小球从飞出到落地所用时间是多少?
(3)在飞行过程中,小球飞行高度何时最大?最大高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:问题情境:在一次综合实践活动课上,同学们以菱形为对象,研究菱形旋转中的问题:已知,在菱形![]() 中,
中,![]() 为对角线,
为对角线,![]() ,
,![]() ,将菱形
,将菱形![]() 绕顶点
绕顶点![]() 顺时针旋转,旋转角为
顺时针旋转,旋转角为![]() (单位
(单位![]() ).旋转后的菱形为
).旋转后的菱形为![]() .在旋转探究活动中提出下列问题,请你帮他们解决.
.在旋转探究活动中提出下列问题,请你帮他们解决.
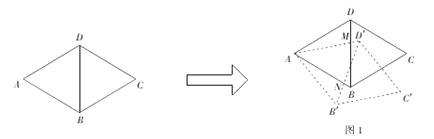
(1)如图1,若旋转角![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .请说明线段
.请说明线段![]() 与
与![]() 的数量关系;
的数量关系;
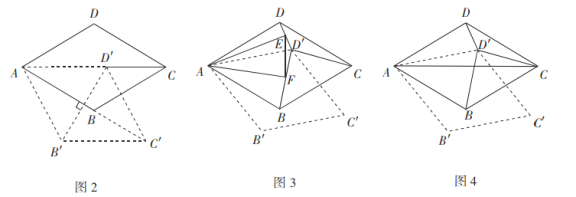
(2)如图2,连接![]() ,菱形
,菱形![]() 旋转的过程中,当
旋转的过程中,当![]() 与
与![]() 互相垂直时,
互相垂直时,![]() 的长为______;
的长为______;
(3)如图3,若旋转角为![]() 时,分别连接
时,分别连接![]() ,
,![]() ,过点
,过点![]() 分别作
分别作![]() ,
,![]() ,连接
,连接![]() ,菱形
,菱形![]() 旋转的过程中,发现在
旋转的过程中,发现在![]() 中存在长度不变的线段
中存在长度不变的线段![]() ,请求出
,请求出![]() 长度;
长度;
操作探究:(4)如图4,在(3)的条件下,请判断以![]() ,
,![]() ,
,![]() 三条线段长度为边的三角形是什么特殊三角形,并说明理由.
三条线段长度为边的三角形是什么特殊三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
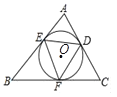
【题目】如图,⊙O是△ABC的内切圆,切点分别相为点D、E、F,设△ABC的面积、周长分别为S、l,⊙O的半径为r,则下列等式:
①∠AED+∠BFE+∠CDF=180°;②S=![]() l r;③2∠EDF=∠A+∠C;④2(AD+CF+BE)=l,其中成立的是( )
l r;③2∠EDF=∠A+∠C;④2(AD+CF+BE)=l,其中成立的是( )
A.①②③④B.②③④C.①③④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
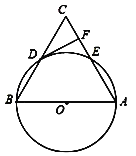
【题目】如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求![]() 的长(结果保留π).
的长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
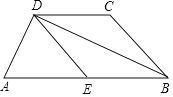
【题目】已知:如图,在梯形ABCD中,AB∥CD,BC=CD,AD⊥BD,E为AB中点.
(1)求证:四边形BCDE是菱形.
(2)若AD=6,BD=8,求四边形BCDE的周长和面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com