
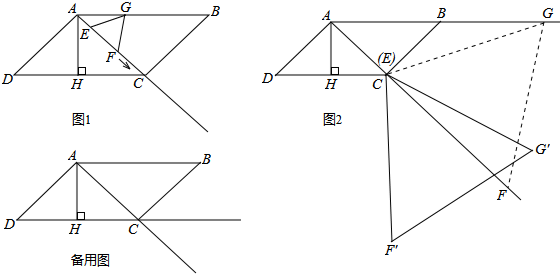
分析 (1)在RT△ADH中,求出DH,HC,即可解决问题.
(2)①当0≤t≤$\frac{7}{3}$时,先证明点G在射线AB上,根据s=S△EGF即可计算.②当$\frac{7}{3}$<t≤4时,作BT∥GF交AC于T,作BL⊥AC于L,MP⊥AC于P,BL⊥AC于L,根据s=S△GEF-S△MCF即可计算.③当4<t≤7时,如图3中,作BM∥GE交AC于M,BL⊥AC于L,KT⊥AC于T,根据s=S△EKC即可计算.
(3)①如图4中,作CK⊥F′G′垂足为K,则CK=7$\sqrt{3}$,由△MCK∽△CAH,得$\frac{CM}{AC}$=$\frac{CK}{AH}$即可解决问题.②如图5中,作CK⊥G′F′垂足为K,由△NCK∽△CAH,得$\frac{KN}{CH}$=$\frac{CK}{AH}$,得NK=14,设CM=MN=a,在RT△CMK中,利用勾股定理即可解决.
解答 解:(1)如图1中,∵AH⊥DC,
∴∠AHD=∠AHC=90°,
∵AD=7.AH=$\sqrt{21}$,
∴DH=$\sqrt{A{D}^{2}-A{H}^{2}}$=$\sqrt{{7}^{2}-(\sqrt{21})^{2}}$=2$\sqrt{7}$,
∵四边形ABCD是平行四边形,
∴AB=CD=4$\sqrt{7}$,
∴DH=HC=2$\sqrt{7}$,∵AH⊥DC,
∴AC=AD=7.
(2)①如图1中,作GK⊥AC于K,
∵AE=t,AF=3t,△GEF是等边三角形,
∴EK=KF=t,AK=2t,GK=$\sqrt{3}$t,
∵AB∥CD,
∴∠BAC=∠ACD,
∴tan∠BAC=tan∠ACH=$\frac{AH}{HC}$=$\frac{\sqrt{3}}{2}$,
∵tan∠GAK=$\frac{GK}{AK}$=$\frac{\sqrt{3}}{2}$,
∴∠BAC=∠GAK,
∴点G在射线AB上.
当0≤t≤$\frac{7}{3}$时,s=$\frac{\sqrt{3}}{4}$•EF2=$\sqrt{3}$t2.
②如图2中,∵∠GAK=∠ACH,∠AKG=∠AHC=90°,
∴△AGK∽△CAH,
∴$\frac{AG}{AC}$=$\frac{AK}{CH}$,
∴AG=$\sqrt{7}$t,
当点G与点B重合时,$\sqrt{7}$t=4$\sqrt{7}$,t=4,
当$\frac{7}{3}$<t≤4时,作BT∥GF交AC于T,作BL⊥AC于L,MP⊥AC于P,BL⊥AC于L
∵S△ACB=$\frac{1}{2}$•AC•BL=$\frac{1}{2}$$•4\sqrt{7}$$•\sqrt{21}$,
∴BL=4$\sqrt{3}$,LT=4,CL=$\sqrt{B{C}^{2}-B{L}^{2}}$=1,
∵MF∥BT,
∴△CMF∽△CBT,
∴$\frac{MP}{BL}$=$\frac{CF}{CT}$,
∴PM=$\frac{4\sqrt{3}}{5}$(3t-7),
∴s=S△GEF-S△MCF=$\frac{\sqrt{3}}{4}$•(2t)2-$\frac{1}{2}$•(3t-7)•$\frac{4\sqrt{3}}{5}$(3t-7)=-$\frac{13}{5}$$\sqrt{3}$t2+$\frac{84\sqrt{3}}{5}$t-$\frac{98\sqrt{3}}{5}$.
③当4<t≤7时,如图3中,作BM∥GE交AC于M,BL⊥AC于L,KT⊥AC于T,
∵△KCE∽△BCM,
∴$\frac{KT}{BL}$=$\frac{CE}{CM}$,
∴KT=$\frac{4\sqrt{3}}{3}$(7-t),
∴s=$\frac{1}{2}$•(7-t)•$\frac{4\sqrt{3}}{3}$(7-t)=$\frac{2\sqrt{3}}{3}$t2-$\frac{28\sqrt{3}}{3}$t+$\frac{98\sqrt{3}}{3}$.
综上所述:s=$\left\{\begin{array}{l}{\sqrt{3}{t}^{2}}&{(0≤t≤\frac{7}{3})}\\{-\frac{13\sqrt{3}}{5}{t}^{2}+\frac{84\sqrt{3}}{5}t-\frac{98\sqrt{3}}{5}}&{(\frac{7}{3}<t≤4)}\\{\frac{2\sqrt{3}}{3}{t}^{2}-\frac{28\sqrt{3}}{3}t+\frac{98\sqrt{3}}{3}}&{(4<t≤7)}\end{array}\right.$.
(3)存在.
①如图4中,作CK⊥F′G′垂足为K,则CK=7$\sqrt{3}$,
∵∠CMK=∠MCN=∠ACH,∠AHC=∠CKM,
∴△MCK∽△CAH,
∴$\frac{CM}{AC}$=$\frac{CK}{AH}$,
∴$\frac{CM}{7}$=$\frac{7\sqrt{3}}{\sqrt{21}}$,
∴CM=7$\sqrt{7}$.
②如图5中, 作CK⊥G′F′垂足为K,
作CK⊥G′F′垂足为K,
∵∠KNC=∠MCN=∠ACH,∠AHC=∠CKN=90°,
∴△NCK∽△CAH,
∴$\frac{KN}{CH}$=$\frac{CK}{AH}$,
∴NK=14,设CM=MN=a,
在RT△CMK中,∵CM2=CK2+KM2,
∴a2=(7$\sqrt{3}$)2+(14-a)2,
∴a=$\frac{49}{4}$.
∴CM=$\frac{49}{4}$,
∴当△CMN是以∠MCN为底角的等腰三角形时,CM=7$\sqrt{7}$或$\frac{49}{4}$.
点评 本题考查几何变换综合题、相似三角形的判定和性质、平行四边形的性质、等边三角形的性质、勾股定理等知识,解题的关键是正确画出图形,学会分类的思想,学会转化的思想,把问题转化为方程解决,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
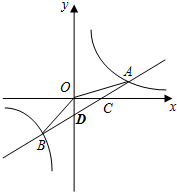 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,与x轴交于点C,与y轴交于点D,已知OA=$\sqrt{10}$,tan∠AOC=$\frac{1}{3}$,点B的坐标为(m,-2).
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,与x轴交于点C,与y轴交于点D,已知OA=$\sqrt{10}$,tan∠AOC=$\frac{1}{3}$,点B的坐标为(m,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
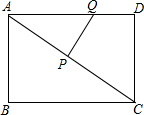 如图,矩形ABCD中,AB=6cm,BC=8cm,动点P从点A出发,在AC上以每秒5cm的速度向点C匀速运动,同时动点Q从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,矩形ABCD中,AB=6cm,BC=8cm,动点P从点A出发,在AC上以每秒5cm的速度向点C匀速运动,同时动点Q从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(0<t<2),连接PQ.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>0 | B. | k<0 | C. | k=0 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com