
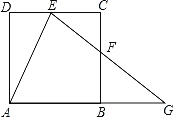
【题目】如图,在正方形ABCD中,点E在DC边上(不与点C,点D重合),点G在AB的延长线上,连结EG,交边BC于点F,且EG=AG,连结AE,AF,设∠AED=![]() ,∠GFB=
,∠GFB=![]() .
.
(1)求![]() ,
,![]() 之间等量关系;
之间等量关系;
(2)若△ADE≌△ABF,AB=2,求BG的长.
【答案】(1)2![]() ﹣
﹣![]() =90°
=90°
(2)![]()
【解析】
(1)由平行线的性质与等腰三角形的性质证明∠AED=∠AEG,再在△BGF中,由三角形的内角和求得![]() 、
、![]() 之间的等量关系;
之间的等量关系;
(2)设BF=x,用x表示EF、FG、BG,进而根据AG=EG列出x的方程求得x便可.
解:(1)∵四边形ABCD是正方形,
∴DC∥AB,∠CBG=∠ABC=90°,
∴∠AED=∠GAE,
∵EG=AG,
∴∠GAE=∠GEA,
∴∠AED=∠AEG=![]() ,
,
∴∠G=180°﹣2![]() ,
,
∵∠BFG+∠G=90°,
∴180°﹣2![]() +
+![]() =90°,
=90°,
∴2![]() ﹣
﹣![]() =90°;
=90°;
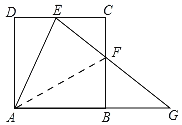
(2)如图,连接AF,∵四边形ABCD是正方形,
∴AB=BC=CD=AD=2,∠C=∠ABC=∠CBG=90°,
设BF=x,
∵△ADE≌△ABF,
∴DE=BF,
∴CE=CF=2﹣x,
∴EF=2![]() x,∠CFE=∠BFG=45°,
x,∠CFE=∠BFG=45°,
∴BG=BF=x,
∴FG=![]() =
=![]() x,
x,
∵AG=EG,
∴2+x=2![]() x+
x+![]() x,
x,
解得,x=2![]() ﹣2,
﹣2,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】 在一个不透明的盒子中装有4小球,4个小球上分别标有数字1,﹣2,3,4,这些小球除标注的数字外其他都相同,将小球搅匀.
(1)从盒子中任意摸出一个小球,恰好摸出标有奇数小球的概率是: ;
(2)先从盒子中任意摸出一个小球,再从余下的3个小球中任意摸出一个小球,请用树状图或列表法求摸出的两个小球标有数字之和大于4的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解九年级男同学1000米跑步的成绩,随机抽取了部分男生进行测试,并将测试成绩分为A、B、C、D四个等级,绘制了不完整的成绩等级频数表和扇形统计图.
成绩等级 | 频数 |
A | 24 |
B | 10 |
C | b |
D | 2 |
合计 | a |
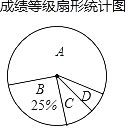
(1)表中a= ,b= ;
(2)扇形图中C的圆心角度数是 ;
(3)若该校共有九年级男生600人,请估计没有获得A等级的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a,b,定义新运算“*”:a*b=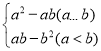 ,例如:4*2,因为4>2,所以4*2=42﹣4×2=8.
,例如:4*2,因为4>2,所以4*2=42﹣4×2=8.
(1)求(﹣7)*(﹣2)的值;
(2)若x1,x2是一元次方程x2﹣5x﹣6=0的两个根,求x1*x2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x+1)(x﹣m)(a为非零常数,1<m<2),当x<﹣1时,y随x的增大而增大,说法正确的是( )
A.若图象经过点(0,1),则﹣![]() <a<0
<a<0
B.若x>﹣![]() 时,则y随x的增大而增大
时,则y随x的增大而增大
C.若(﹣2020,y1),(2020,y2)是函数图象上的两点,则y1<y2
D.若图象上两点(![]() ,y1),(
,y1),(![]() +n,y2)对一切正数n,总有y1>y2,则
+n,y2)对一切正数n,总有y1>y2,则![]() ≤m<2
≤m<2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P为某个封闭图形边界上的一定点,动点M从点P出发,沿其边界顺时针匀速运动一周,设点M的运动时间为x,线段PM的长度为y,表示y与x的函数图象大致如图所示,则该封闭图形可能是( )
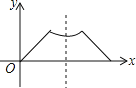
A. 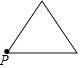 B.
B.  C.
C. 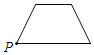 D.
D. 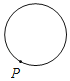
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.
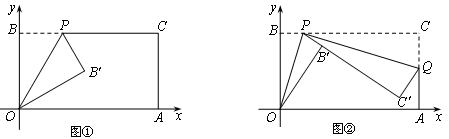
(Ⅰ)如图①,当∠BOP=300时,求点P的坐标;
(Ⅱ)如图②,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,若AQ=m,试用含有t的式子表示m;
(Ⅲ)在(Ⅱ)的条件下,当点C′恰好落在边OA上时,求点P的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行统计,结果如下表,并绘制了如下尚不完整的统计图,已知![]() ,
,![]() 两组发言的人数比为5:2,请结合图表中相关数据回答下列问题:
两组发言的人数比为5:2,请结合图表中相关数据回答下列问题:
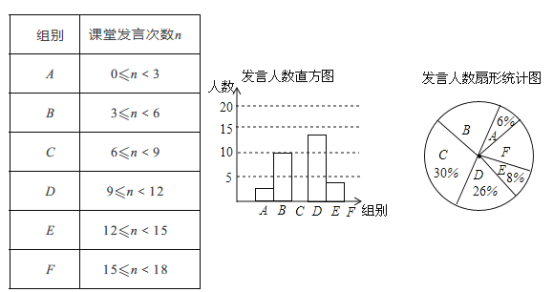
(1)本次抽样的学生人数为_________;
(2)补全条形统计图;
(3)该年级共有学生500人,请估计这天全年级发言次数不少于12的人数;
(4)已知![]() 组发言的学生中有1位女生,
组发言的学生中有1位女生,![]() 组发言的学生中有2位男生,现从
组发言的学生中有2位男生,现从![]() 组与
组与![]() 组中分别抽一位学生写报告,请用树状图或列表法,求所抽到的两位学生恰好是一男一女的概率.
组中分别抽一位学生写报告,请用树状图或列表法,求所抽到的两位学生恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
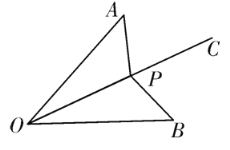
【题目】如图,已知射线OC为∠AOB的平分线,且OA=OB,点P是射线OC上的任意一点,连接AP、BP.
(1)求证:△AOP≌△BOP;
(2)若∠AOB=50°,且点P是△AOB的外心,求∠APB的度数;
(3)若∠AOB=50°,且△OAP为钝角三角形,直接写出∠OAP的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com