
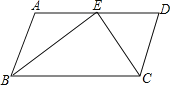
【题目】如图,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,点
,点![]() 在
在![]() 上,求证:
上,求证:![]() .
.
【答案】详见解析
【解析】
在BC上取点F,使BF=BA,连接EF,由角平分线的性质可以得出∠1=∠2,从而可以得出△ABE≌△FBE,可以得出∠A=∠5,进而可以得出△CDE≌△CFE,就可以得出CD=CF,即可得出结论.
在BC上取点F,使BF=BA,连接EF,
∵BE、CE分别是∠ABC和∠BCD的平分线,
∴∠1=∠2,∠3=∠4,
在△ABE和△FBE中,
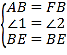 ,
,
∴△ABE≌△FBE(SAS),
∴∠A=∠5,
∵AB∥CD,
∴∠A+∠D=180°,
∴∠5+∠D=180,
∵∠5+∠6=180°,
∴∠6=∠D,
在△CDE和△CFE中,
 ,
,
∴△CDE≌△CFE(AAS),
∴CF=CD.
∵BC=BF+CF,
∴BC=AB+CD.



科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,AB=8cm,AC=4cm,△BAC的平分线AD与BC的垂直平分线DG交于点D,过点D的直线DE⊥AB于点E,DF⊥AC于点F.
(1)求证:BE=CF;
(2)求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元。
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在数轴上![]() ,
,![]() 两点对应数分别为-3,20.
两点对应数分别为-3,20.
(1)若![]() 点为线段
点为线段![]() 的中点,求
的中点,求![]() 点对应的数.
点对应的数.
(2)若点![]() 以每秒3个单位,点
以每秒3个单位,点![]() 以每秒2个单位的速度同时出发向右运动多长时间后
以每秒2个单位的速度同时出发向右运动多长时间后![]() ,
,![]() 两点相距2个单位长度?
两点相距2个单位长度?
(3)若点![]() ,
,![]() 同时分别以2个单位长度秒的速度相向运动,点
同时分别以2个单位长度秒的速度相向运动,点![]() (
(![]() 点在原点)同时以4个单位长度/秒的速度向右运动.
点在原点)同时以4个单位长度/秒的速度向右运动.
①经过![]() 秒后
秒后![]() 与
与![]() 之间的距离
之间的距离![]() (用含
(用含![]() 的式子表示)
的式子表示)
②几秒后点![]() 到点
到点![]() 、点
、点![]() 的距离相等?求此时
的距离相等?求此时![]() 对应的数.
对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了《整式的乘除》这一章之后,小明联想到小学除法运算时,会碰到余数的问题,那么类比多项式除法也会出现余式的问题.例如,如果一个多项式(设该多项式为![]() )除以
)除以![]() 的商为
的商为![]() ,余式为
,余式为![]() ,那么这个多项式是多少?他通过类比小学除法的运算法则:被除数=除数×商+余数,推理出多项式除法法则:被除式=除式×商+余式.
,那么这个多项式是多少?他通过类比小学除法的运算法则:被除数=除数×商+余数,推理出多项式除法法则:被除式=除式×商+余式.
请根据以上材料,解决下列问题:
(1)请你帮小明求出多项式;
(2)小明继续探索,如果一个多项式除以![]() 商为
商为![]() ,余式为
,余式为![]() ,请你根据以上法则求出该多项式;
,请你根据以上法则求出该多项式;
(3)上述过程中,小明把小学的除法运算法则运用在多项式除法运算上,这里运用的数学思想是_____.
A.类比思想 B.公理化思想 C.函数思想 D.数形结合思想
查看答案和解析>>
科目:初中数学 来源: 题型:
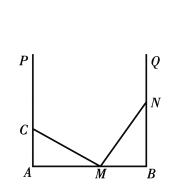
【题目】在学习完“探索三角形全等的条件”一节后,小丽总结出很多全等三角形的模型,她设计了以下问题给同桌解决:做一个“![]() ”字形框架
”字形框架![]() 其中
其中![]() 足够长,
足够长,![]() 于点
于点![]() 于点
于点![]() 点
点![]() 从
从![]() 出发向
出发向![]() 运动,点
运动,点![]() 从
从![]() 出发向
出发向![]() 运动, 速度之比为
运动, 速度之比为![]() 运动到某一瞬间两点同时停止,在
运动到某一瞬间两点同时停止,在![]() 上取点
上取点![]() 使
使![]() 与
与![]() 全等,则
全等,则![]() 的长度为________________
的长度为________________![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
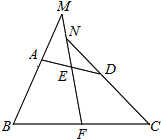
【题目】如图,在四边形ABCD中,E、F分别是AD、BC的中点,连接FE并延长,分别交CD的延长线于点M、N,∠BME=∠CNE,求证:AB=CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE___CF;(填“>”,“<”或“=”);EF,BE,AF三条线段的数量关系是:___.
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件___,使①中的两个结论仍然成立,并证明两个结论成立。
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想并证明。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com