
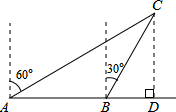
 如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,求海岛C到航线AB的距离CD.
如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,求海岛C到航线AB的距离CD. 分析 根据方向角的定义及余角的性质求出∠CAD=30°,∠CBD=60°,再由三角形外角的性质得到∠CAD=30°=∠ACB,根据等角对等边得出AB=BC=20,然后解Rt△BCD,求出CD的长即可.
解答 解:根据题意可知∠CAD=30°,∠CBD=60°,
∵∠CBD=∠CAD+∠ACB,
∴∠CAD=30°=∠ACB,
∴AB=BC=20海里,
在Rt△CBD中,∠BDC=90°,∠DBC=60°,sin∠DBC=$\frac{DC}{BC}$,
∴sin60°=$\frac{DC}{BC}$,
∴CD=12×sin60°=20×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$(海里).
答:海岛C到航线AB的距离CD长为10$\sqrt{3}$海里.
点评 本题考查了解直角三角形的应用-方向角问题,难度适中,解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,利用锐角三角函数的定义求解.


科目:初中数学 来源: 题型:解答题
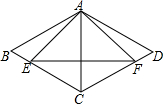 如图,在菱形ABCD中,E、F分别为边BC、CD上一点且BE=DF.
如图,在菱形ABCD中,E、F分别为边BC、CD上一点且BE=DF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
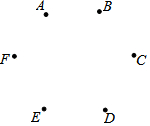 如图,已知点A,B,C,D,E,F最边长为1的正六边形的顶点,在连接两点所得的所有线段中任取一条线段,取到长度为$\sqrt{3}$的线段的概率为( )
如图,已知点A,B,C,D,E,F最边长为1的正六边形的顶点,在连接两点所得的所有线段中任取一条线段,取到长度为$\sqrt{3}$的线段的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{2}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若|x|=|y|,则x=y | B. | 若x2=y2,则x=y | C. | 若$\sqrt{x^2}=|y|$,则x=y | D. | 若$\root{3}{x}=\root{3}{y}$,则x=y |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
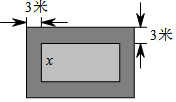 一标志性建筑的底面呈长方形,长是宽的2倍,在其四周铺上花岗岩,形成一个边宽为3米的长方形框(如图所示).已知铺这个框恰好用了504块边长为0.5米的正方向花岗岩(接缝忽略不计).若设此标志性建筑底面长方形的宽为x米,给出下列方程:
一标志性建筑的底面呈长方形,长是宽的2倍,在其四周铺上花岗岩,形成一个边宽为3米的长方形框(如图所示).已知铺这个框恰好用了504块边长为0.5米的正方向花岗岩(接缝忽略不计).若设此标志性建筑底面长方形的宽为x米,给出下列方程:| A. | ② | B. | ③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
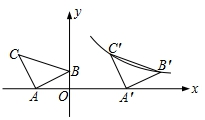 如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(-2,0),B(0,1).
如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(-2,0),B(0,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com