
【题目】如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(﹣1,0)与点C(x2 , 0),且与y轴交于点B(0,﹣2),小强得到以下结论:①0<a<2;②﹣1<b<0;③c=﹣1;④当|a|=|b|时x2> ![]() ﹣1;以上结论中正确结论的序号为 .
﹣1;以上结论中正确结论的序号为 . 
【答案】①④
【解析】解:由A(﹣1,0),B(0,﹣2),得b=a﹣2,
∵开口向上,
∴a>0;
∵对称轴在y轴右侧,
∴﹣ ![]() >0,
>0,
∴﹣ ![]() >0,
>0,
∴a﹣2<0,
∴a<2;
∴0<a<2;
∴①正确;
∵抛物线与y轴交于点B(0,﹣2),
∴c=﹣2,故③错误;
∵抛物线图象与x轴交于点A(﹣1,0),
∴a﹣b﹣2=0,
∵0<a<2,
∴0<b+2<2,
﹣2<b<0,故②错误;
∵|a|=|b|,二次函数y=ax2+bx+c的对称轴在y轴的右侧,
∴二次函数y=ax2+bx+c的对称轴为x= ![]() ,
,
∴x2=2> ![]() ﹣1,故④正确.
﹣1,故④正确.
故答案为:①④.
根据抛物线与y轴交于点B(0,-2),可得c=-2,可对③作出判断;由抛物线图象与x轴交于点A(-1,0),可得a-b-2=0,结合对称轴的位置,可对①②作出判断;由|a|=|b|可得二次函数y=ax2+bx+c的对称轴为x=![]() 可得x2=2,比较大小即可对④作出判断;从而得出答案。
可得x2=2,比较大小即可对④作出判断;从而得出答案。


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
【题目】有大小两种货车,已知1辆大货车与3辆小货车一次可以运货14吨,2辆大货车与5辆小货车一次可以运货25吨.
(1)1辆大货车与1辆小货车一次可以运货各多少吨?
(2)1辆大货车一次费用为300元,1辆小货车一次费用为200元,要求两种货车共用10辆,两次完成80吨的运货任务,且总费用不超过5400元,有哪几种用车方案?请指出费用最低的一种方案,并求出相应的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:小明遇到这样一个问题;△ABC中,有两个内角相等.
①若∠A=110°,求∠B的度数;
②若∠A=40°,求∠B的度数.
小明通过探究发现,∠A的度数不同,∠B的度数的个数也可能不同,因此为同学们提供了如下解题的想法:
对于问题①,根据三角形内角和定理,∵∠A=110°>90°,∠B=∠C=35°;
对于问题②,根据三角形内角和定理,∵∠A=40°<90°,∴∠A=∠B或∠A=∠C或∠B=∠C,∴∠B的度数可求.请回答:
(1)问题②中∠B的度数为 ;
(2)参考小明解决问题的思路,解决下面问题:
△ABC中,有两个内角相等.设∠A=x°,当∠B有三个不同的度数时,求∠B的度数(用含x的代式表示)以及x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若x1 , x2(x1<x2)是方程(x﹣a)(x﹣b)=﹣1(a<b)的两根,则实数x1 , x2 , a,b的大小关系是( )
A.a<x1<x2<b
B.x1<a<x2<b
C.x1<a<b<x2
D.x1<x2<a<b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A、B,C三点的坐标分别为(0,1)、(3,3)、(4,0).
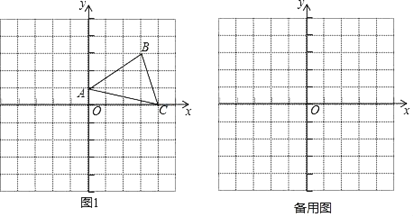
(I)S△AOC= ;
(2)若点P(m﹣1,1)是第二象限内一点,且△AOP的面积不大于△ABC的面积,求m的取值范围;
(3)若将线段AB向左平移1个单位长度,点D为x轴上一点,点E(4,n)为第一象限内一动点,连BE、CE、AC,若△ABD的面积等于由AB、BE、CE、AC四条线段围成图形的面积,则点D的坐标为 .(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市“精准扶贫”工作中,甲、乙两个工程队先后接力为扶贫村庄修建一条210米长的公路,甲队每天修建15米,乙队每天修建25米,一共用10天完成.
根据题意,小红和小芳同学分别列出了下面尚不完整的方程组:
小红:![]() 小芳:
小芳:
(1)请你分别写出小红和小芳所列方程组中未知数x,y表示的意义:
小红:x表示______,y表示______;
小芳:x表示______,y表示______;
(2)在题中“( )”内把小红和小芳所列方程组补充完整;
(3)甲工程队一共修建了______天,乙工程队一共修建了______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一件工艺品的进价为100元,标价135元出售,每天可售出100件,根据销售统计,一件工艺品每降价1元,则每天可多售出4件,要使每天获得的利润最大,则每件需降价( )
A.3.6 元
B.5 元
C.10 元
D.12 元
查看答案和解析>>
科目:初中数学 来源: 题型:
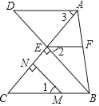
【题目】如图,BE⊥AC与点E,MN⊥AC于点N,∠1=∠2,∠3=∠C,若∠AFE=80°,求∠DAF的度数.请根据解题过程“填空”或“说明理由”.
解:∵BE⊥AC,MN⊥AC
∴BE∥MN
∴∠1= ( )
又∵∠1=∠2
∴∠2= ( )
∴EF∥BC( )
∵∠3=∠C
∴AD∥BC
∴AD∥EF
∴∠DAF+∠AFE=180°( )
∴∠DAF=180°﹣∠AFE=180°﹣80°=100°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com